看到题解里面还没有用STL vector做的，所以我就来交一发。

题目链接

1：转化题意

在一张图中，一共有 pp 个节点，cc 条双向边，有 nn 个节点不能删除，求出最少需要删除多少个节点才能使得这 nn 个固定点都到达不了11号节点。

2：分析和建模

在完成题意的转化之后，我们发现题目要让我们删除一些点（尽量少），使得整张图变成两个不连通的部分，网络流算法中的最小割（最大流）算法可以处理这这个问题。

【不熟悉最大流算法的同学可以先做一下模板题】
最大流模板

但是我们又发现，一般的最小割处理的是 “删除图的一部分边使得图的两部分变得不连通” 而这道题目让我们删除的是图中一部分节点。于是我们就需要把节点转换成边。

我使用的方法是把每一个节点拆分成两个节点（出点和入点），具体的做法可以参考
P1345 奶牛的电信Telecowmunication
这道题中的题解。

这里来简单解释一下这种做法：首先，我们把图中的每一个点拆分成两个点：出和入点。

并且这两个节点之间有一条单向边连接

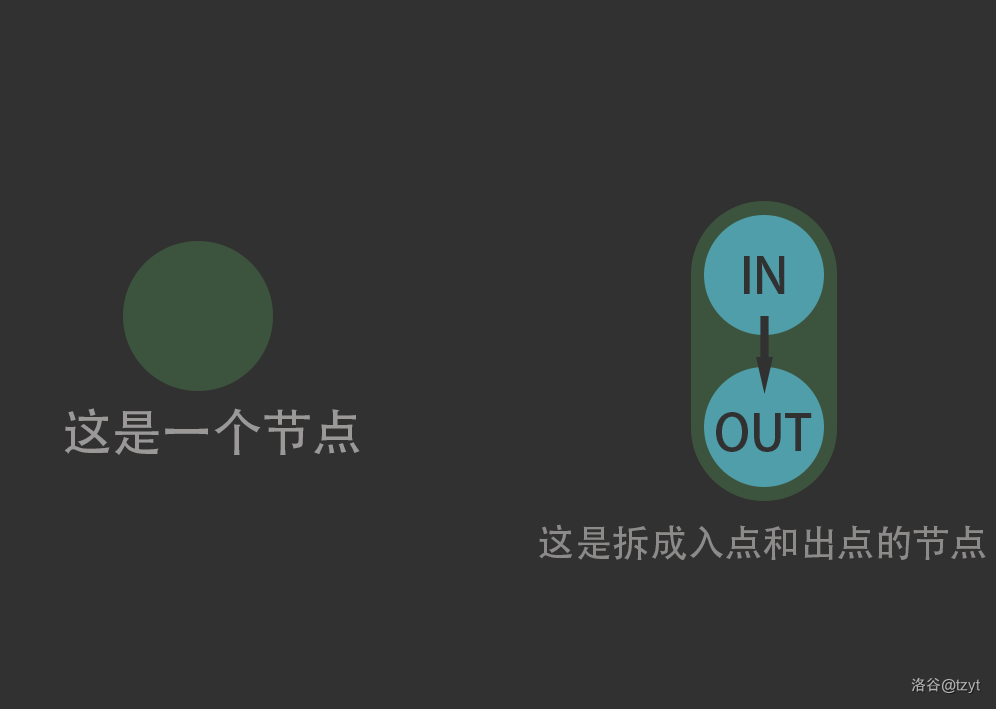
每条指向这个点的有向边都只能连接这个点的入点。并且从这个节点出发的有向边都只能从它的出点出发。

那么，把每个节点分成出点和入点之后有什么用呢？在一般的最小割问题中，如果我们想知道要取消掉多少条边，可以使得这张图的汇点和源点不连通，就可以把每条边的权值设置为11，并且可以付出11的代价删除这条边。

在以割点为基础的最小割问题中，我们可以把每个节点中连接出点和入点的那条边的权值设置为11。这样子如果我们想要删除这个节点，就可以付出11的代价，把这条边切断，这个点也就被删除了。

那么问题就来了，这道题目中明确的说明了有一些节点是不能删除的，如果都把权值设置成11，如何处理不能删除的节点呢？

对于这些关键节点（不能删除的点），我们可以把他们的内部权值设置成 INFINF，这样就不会把这些点删掉了（最小割算法计算的是付出最小的代价使图变得不连通，而设置成 INFINF 会让删掉这个点变得很不合算）。

另外，我们需要注意，除了题目中说的关键点，源点和汇点也是不能删除的，所以在建图的时候需要处理一下。并且题目让我们求的是最少删去多少个节点，所以连接这些节点的边也是不能删除的，需要把容量设置成 INFINF。

解决了边的容量问题后我们再来考虑源点和汇点，我们可以把11号节点设置成源点，把所有关键点连接到汇点上，这样子求出的答案就是让所有关键点都到达不了11号节点的最小删除节点数（如果任何一个关键点可以到达一号节点，那么汇点也可以到达11号节点）。

建图步骤总结：

  1. 把每个节点拆成入点和出点，中间连一条内部边
  2. 对于能删除的点，内部边的容量设置成11
  3. 对于不能删除的点，内部边容量设置成 INFINF
  4. 不能删除的边包括：
    1. 源点的内部边
    2. 汇点的内部边
    3. 连接每个节点的边
    4. 关键点的内部边
  5. 源点设置成11号节点，汇点连接所有的关键点

3：算法

我采用的是dinic算法，因为每次增广可以找到多条增广路，所以算法的速度会比EK算法高一些，不熟悉这个算法的同学可以去看一下之前提到的最大流模板题的题解。

4.代码实现及细节

在实现拆分节点这个操作的时候，我们可以把一个节点的入点的编号设置成它本身的编号，而出点的编号就设置成本身的编号 + pp（节点总数），这样子可以确保不会重复。

在实现dinic算法时，需要进行对反向边的操作，我使用的是STL vector来存边，因此需要在node结构体中加入rev（reverse）变量，记录当前边的反向边的下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include <bits/stdc++.h>
using namespace std;
const int MAXM = 100000;
const int INF = 0x3f3f3f3f;
struct node
{
    int to, mflow, rev; //to连接的下个节点的编号
                        //mflow(maxflow)记录当前边的容量
                        //rev(reverse)记录当前边的反向边的下标
};
int p, c, n, s, t;
vector<node> edge[MAXM];
int g_farm[MAXM];                            //完好的农场（关键点）
int layer[MAXM];                             //每个节点的层数
node assign_node(int to, int mflow, int rev) //赋值函数
{
    node temp;
    temp.to = to, temp.mflow = mflow, temp.rev = rev;
    return temp;
}

void add_edge(int from, int to, int mflow) //加边
{
    edge[from].push_back(assign_node(to, mflow, edge[to].size()));   //不需要-1是因为edge[to]还没有push过 from这个节点
    edge[to].push_back(assign_node(from, 0, edge[from].size() - 1)); //-1是因为vector的下标是从0开始的，而.size()会返回元素的数量
}

namespace dinic
{
    bool layering() //分层
    {
        bool vis[MAXM];
        memset(vis, false, sizeof(vis));
        memset(layer, 0, sizeof(layer));
        queue<int> q;
        vis[s] = true;
        layer[s] = 1;
        q.push(s);
        while (!q.empty())
        {
            int cur = q.front();
            q.pop();
            for (auto nex : edge[cur]) //c++11的新特性，意思是用nex遍历edge[cur]中的所有元素
            {
                if (nex.mflow > 0 && vis[nex.to] == false)
                {
                    layer[nex.to] = layer[cur] + 1;
                    q.push(nex.to);
                    vis[nex.to] = true;
                }
            }
        }
        return (layer[t] != 0); //返回分层操作是否成功（是否能从源点到达汇点）
    }

    int find_aug_path(int cur, int cur_flow) //寻找增广路
    {
        if (cur == t)
        {
            return cur_flow;
        }
        int ans = 0;
        for (int i = 0; i < int(edge[cur].size()); i++)
        {
            if (edge[cur][i].mflow > 0 && layer[edge[cur][i].to] == layer[cur] + 1)
            {
                int nex_flow = find_aug_path(edge[cur][i].to, min(cur_flow, edge[cur][i].mflow));
                edge[cur][i].mflow -= nex_flow;                            //正向边
                edge[edge[cur][i].to][edge[cur][i].rev].mflow += nex_flow; //反向边
                cur_flow -= nex_flow;
                ans += nex_flow;
                if (cur_flow <= 0) //如果当前的容量已经不够了，就直接返回来节省时间
                {
                    return ans;
                }
            }
        }
        return ans;
    }

    int find_maxflow()
    {
        int ans = 0;
        while (layering())
        {
            ans += find_aug_path(s, INF);
        }
        return ans;
    }
}

void input_creat() //输入和建图
{
    scanf("%d%d%d", &p, &c, &n);
    s = 0, t = 2 * p + 1;
    add_edge(0, 1, INF);     //再搞一个点接入源点的入点，容量也要设成INF
    add_edge(1, 1 + p, INF); //源点的入点和出点设置成INF
    for (int i = 1; i <= c; i++)
    {
        int from, to;
        scanf("%d%d", &from, &to);
        add_edge(from + p, to, INF); //from的出点和to的入点相连
        add_edge(to + p, from, INF); //to的出点和from的入点相连
    }
    for (int i = 1; i <= n; i++)
    { //n是不能割的点
        int point;
        scanf("%d", &point);
        add_edge(point + p, t, INF);     //把所有关键点连接到汇点
        add_edge(point, point + p, INF); //所有关键点的内部边的容量都要设成INF
        g_farm[point] = 1;               //标记关键点
    }
    for (int i = 2; i <= p; i++)
    {
        if (!g_farm[i])
        {
            add_edge(i, i + p, 1); //除了关键点的其他点可以删，所以内部边的容量设成1
        }
    }
}

main()
{
    input_creat();
    printf("%d", dinic::find_maxflow());
    system("pause");
}

第一次写题解，问题可能比较多，如果看到题解有什么不对的欢迎在评论区提出，或者私信我，有看不懂的地方也欢迎提问。最后，如果这篇题解对你有帮助就点个赞吧，或者在评论区中交流你的看法。