因为学校里的各种事情，以及复习考试，自从上次更新博客已经是四个多月的事情了，距离上次写图形学的博客那就更久了。

最近刚放暑假把之前只看了光线追踪部分的 GAMES101 完整的学习了一遍，还是非常惊喜的：很多之前不太清楚的概念（特别是数学方面的）过了一段时间再看又有了些新的理解。因为课程时间限制的问题，有有部分内容没有比较详细的讲，这里记录一些我自己的理解。

三维旋矩阵

这个东西我已经在之前 RT: The Next Week 的文章中写过了，不过之前的解释比较。。。怪，很啰嗦，并且没有从坐标系变换的角度来解释，这里就重新写下（当然我还没有系统的学过线性代数，所以以下内容可能还是很扯）。

绕三个轴的三维旋转矩阵分别可以写作下列的形式：

Rx(θ)=[1000cos⁡θ−sin⁡θ0sin⁡θcos⁡θ]R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{bmatrix}

Rz(θ)=[cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001]R_z(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix}

Ry(θ)=[cos⁡θ0sin⁡θ010−sin⁡θ0cos⁡θ]R_y(\theta) = \begin{bmatrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{bmatrix} \\

不难发现，绕 y 轴旋转的矩阵中，sin⁡θ\sin \theta 和 −sin⁡θ-\sin \theta 的位置似乎是反的，非常奇怪。原视频中，旋转矩阵是通过选取一些特殊点完成推导的，这里我感觉用坐标系变换的方法更加易于理解（虽然闫老师觉的这个更复杂）。

首先看绕 z 轴的，这个比较简单，基本上就是二维旋转矩阵的情况：

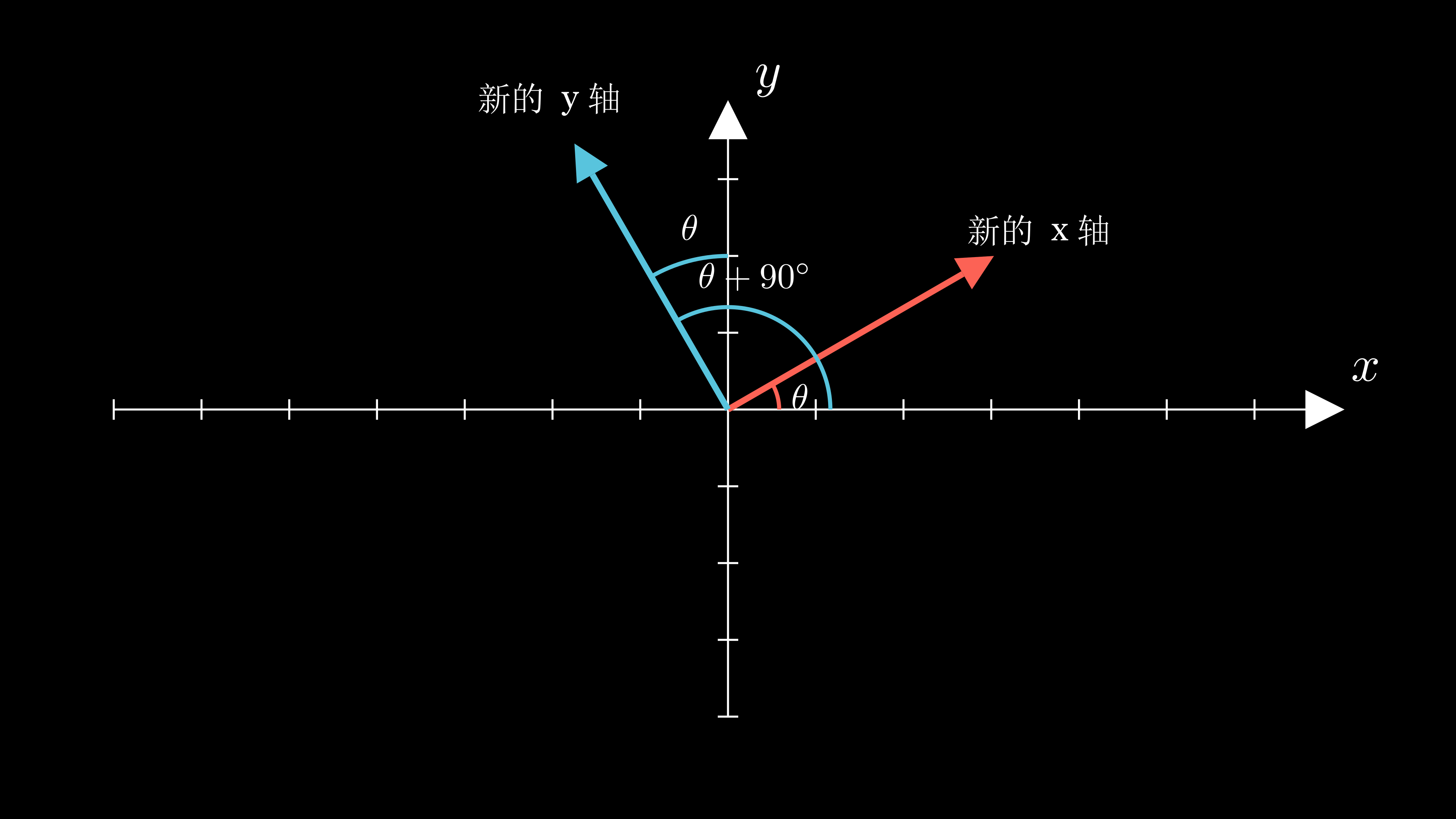
注意这里我虽然没有加入 z 轴，但是通过右手定则，可以发现 z 轴是朝着穿出屏幕方向的。

我们可以分别把新 x 轴 （i^\hat i） 和新 y 轴（j^\hat j）用向量形式表示出来，注意这里这两个向量都是单位向量：

i^=[cos⁡θsin⁡θ0]\hat i = \begin{bmatrix} \cos \theta \\ \sin \theta \\ 0 \end{bmatrix} \\

观察 j^\hat j 和原 y 轴的夹角，可以发现是 θ\theta，所以可以把 i^\hat i 的向量形式“反”一下。还有一点需要注意的是：j^\hat j 的 x 分量是负数：

j^=[−sin⁡θcos⁡θ0]\hat j = \begin{bmatrix} -\sin \theta \\ \cos \theta \\ 0 \end{bmatrix} \\

其实不管在什么坐标系中，任何坐标都是通过单位向量乘以一些长度得到的（可以想象成一个点在某个方向移动一些距离）。比如在平面直角坐标系中，(1,2)(1, 2) 的坐标就可以理解成，把一个点向着 x 方向移动 1，向着 y 方向移动 2。

所以，在旋转过后的坐标系，对于一个点 (x,y,z)(x, y, z)，他的新坐标就是 (xi^,yj^,z)(x\hat i, y\hat j, z)。相当于是向着 i^\hat i 方向移动了 x 个单位，向着 j^\hat j 方向移动了 y 个单位，以及向原来的 z 方向（虽然没有变换，但是这里我们还是把它标记成 k^\hat k）移动了 z 个单位。

所以新的坐标就是：

p=x[cos⁡θsin⁡θ0]+y[−sin⁡θcos⁡θ0]+z[001]p = x\begin{bmatrix} \cos \theta \\ \sin \theta \\ 0 \end{bmatrix} + y\begin{bmatrix} -\sin \theta \\ \cos \theta \\ 0 \end{bmatrix} + z\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}

观察之前提供的旋转矩阵公式，能发现 RzR_z 确实能满足上式：

[cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001][xyz]=x[cos⁡θsin⁡θ0]+y[−sin⁡θcos⁡θ0]+z[001] \begin{bmatrix} \textcolor{red}{\cos \theta} & \textcolor{blue}{-\sin \theta} & \textcolor{green}{0} \\ \textcolor{red}{\sin \theta} & \textcolor{blue}{\cos \theta} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{0} & \textcolor{green}{1} \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = x\textcolor{red}{\begin{bmatrix} \cos \theta \\ \sin \theta \\ 0 \end{bmatrix}} + y \textcolor{blue}{\begin{bmatrix} -\sin \theta \\ \cos \theta \\ 0 \end{bmatrix} } + z\textcolor{green}{\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}}

这里有一个比较有意思的地方，已经通过不同的颜色标记出来了：可以发现，旋转矩阵中的三列分别对应着 i^\hat i，j^\hat j 和 k^\hat k，也就是新坐标系中的三个轴的方向。

这样一来，从坐标系变换的角度，就非常容易理解为什么旋转矩阵是这么写的了。我们可以直接把变换后的三个轴的方向写到矩阵中的三列，从而得到旋转矩阵。

我们可以用相同的方法来分析绕 y 轴的旋转，就是那个看起来“反”了的矩阵。

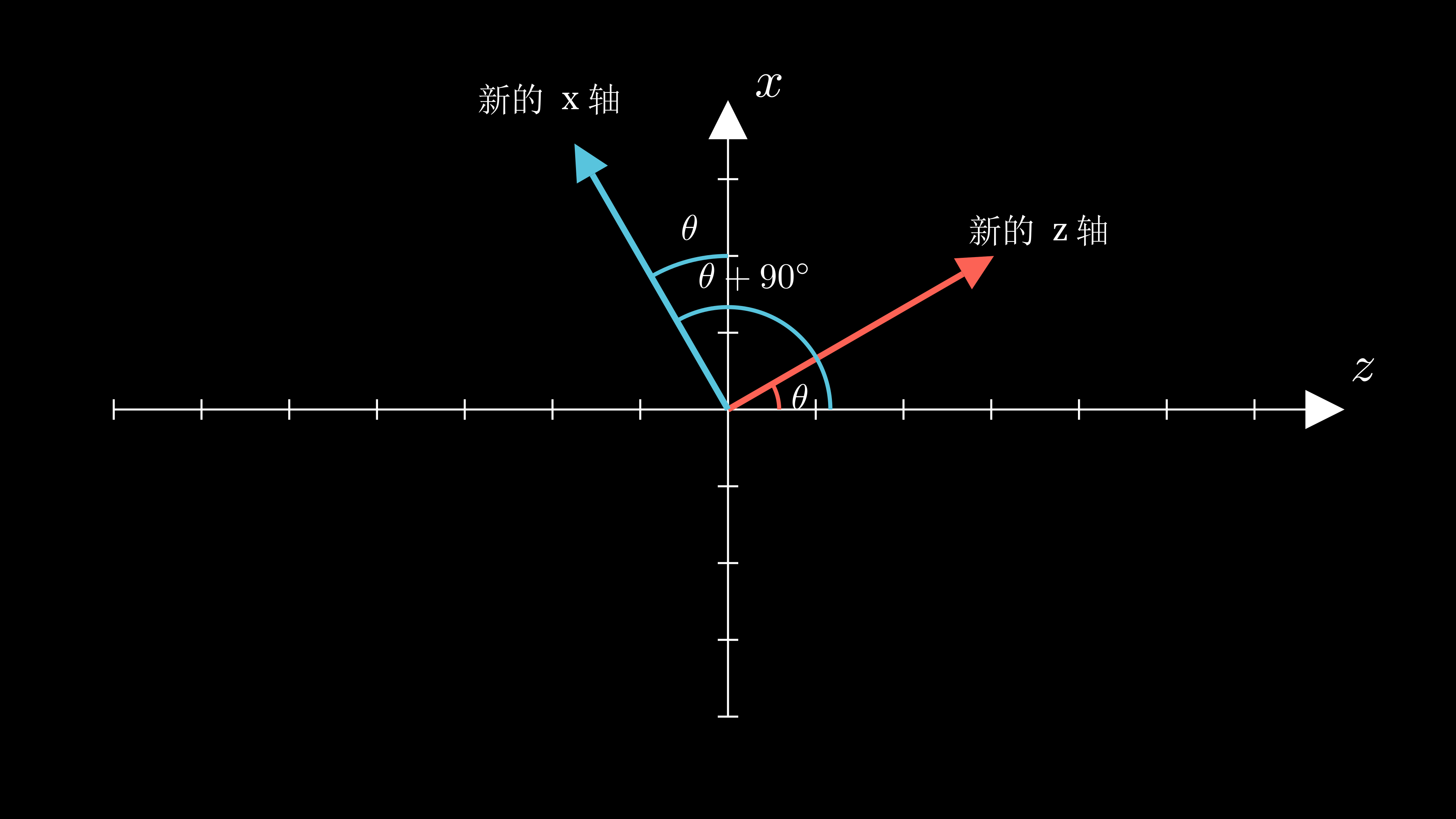
虽然看起来和刚刚的图很相似，但是可以发现图中的标签已经变过了。同样，通过右手定则，可以发现这时 y 轴是朝着穿出屏幕方向的。

那么有了刚刚的观察，现在我们只需要找到当前情况下的 i^,j^,k^\hat i, \hat j, \hat k 就可以写出绕 y 轴的旋转矩阵了。

首先，对于新的 z 轴，也就是 k^\hat k，我们可以类比绕 z 轴情况下的 i^\hat i，它的向量形式如下：

k^=[sin⁡θ0cos⁡θ]\hat k = \begin{bmatrix} \sin \theta \\ 0 \\ \cos \theta \end{bmatrix} \\

这里 y 分量为 0 的原因很明显，因为我们考虑的是绕 y 轴旋转，所以 y 肯定没有变化。

然后，类比绕 z 轴情况下的 j^\hat j，我们可以得到 i^\hat i 的向量形式：

i^=[cos⁡θ0−sin⁡θ]\hat i = \begin{bmatrix} \cos \theta \\ 0 \\ -\sin \theta \end{bmatrix} \\

对于 j^\hat j，因为和原来没有变化，所以可以简单的写作：

j^=[010]\hat j = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \\

合并这些表示新 x，y，z 方向的向量，可以得到：

[i^ ∣ j^ ∣ k^]=[cos⁡θ0sin⁡θ010−sin⁡θ0cos⁡θ]\left[\hat i \ | \ \hat j \ | \ \hat k\right] = \begin{bmatrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{bmatrix} \\

重心坐标

和 GAMES101 课程中讲的一样，重心坐标（特别是三角形的）在图形学中非常有用，可以很方便的把三角形节点上的信息插值到三角形面上。

我最初听课的时候还是有较多疑惑的，比如为什么一定要三个系数和相加等于 1，并且三个系数都不为负数，某个点才是在三角形内部的呢？

后来思考了一段时间，感觉用“顾名思义”的方式理解这个概念是直观的，也就是从重心的角度去理解。

物理角度

假设有一个三角形，其三个顶点的质量分别为 Ma,Mb,McM_a, M_b, M_c，并且除了顶点外，别的区域质量均为 0，那么根据重心的定义，三角形的重心就是：

重心=MaA+MbB+McCMa+Mb+Mc\text{重心} = \frac{M_aA + M_bB + M_cC}{M_a + M_b + M_c}

把这三个项分开，可以得到：

AMaMa+Mb+Mc+BMbMa+Mb+Mc+CMcMa+Mb+McA\frac{M_a}{M_a + M_b + M_c} + B\frac{M_b}{M_a + M_b + M_c} + C\frac{M_c}{M_a + M_b + M_c}

这个形式简直和重心坐标的 αA+βB+γC\alpha A + \beta B + \gamma C 太相似了，每项都是一个系数乘以一个顶点的坐标。

观察形如 MaMa+Mb+Mc\frac{M_a}{M_a + M_b + M_c} 的项，可以发现，计算重心时的系数完全符合重心坐标的要求，即 α+β+γ=1\alpha + \beta + \gamma = 1，并且每项不是负数。

现在用物理上重心的思路来思考，我们在转换普通坐标到重心坐标时到底在转换什么？

把重心公式的系数对应到重心坐标的系数，也就是 MaMa+Mb+Mc→α\frac{M_a}{M_a + M_b + M_c} \to \alpha，我们能发现，这些系数实际上是三角形每个顶点的质量占总质量的比例。

也就是说，在转换的过程中（假设把 pp 点从笛卡尔坐标系转换到重心坐标系），我们实际上计算的是这样一个问题：三角形的三个顶点如何分配重量，才能使得三角形的重心位于 pp 点？

转换后的坐标，(α,β,γ)(\alpha, \beta, \gamma) 其实就是在三角形三个顶点上分配的重量的比例。

这样一来，我们就很容易理解这三个数为什么符合相加为 1 并且非负才能使点在三角形内部的要求了。首先，从物理的角度来思考，如果质量非负，那么重心一定在物体的内部。其次，如果要符合重心的定义，那么 α,β,γ\alpha, \beta, \gamma 相加一定是等于 1 的。因为它们三个代表的是三个顶点的质量占总质量的比例，所以这三个数字相加一定是 1（对应总质量）。

当然，重心坐标是由物理上的定义推广出来的，所以用纯代数的方法来说明可能更有说服力。

代数角度

我们知道，三角形的重心坐标就是三个顶点的线性组合来标记一个坐标，也就是 p=αA+βB+γCp = \alpha A + \beta B + \gamma C。现在我们可以尝试用代数的方式来说明，为什么这三个系数相加等于 1 并且非负才能使点在三角形内部。

首先，我们可以把 pp 点用另一种方式表示出来，这对之后的推导会有帮助：

p=A+uAB→+vAC→p = A + u\overrightarrow{AB} + v\overrightarrow{AC}

注意这里的 uu 和 vv 其实和重心坐标的三个系数没有关系，这个式子的含义是：从 A 点出发，沿着 AB 方向走 uu 个单位，然后沿着 AC 方向走 vv 个单位，就可以到达 pp 点。

首先，如果要让点在三角形内部，有一点是可以确定的：uu 和 vv 是非负的，因为考虑当前在 A 点上，只向着 BA→\overrightarrow{BA} 或者 CA→\overrightarrow{CA} 方向走任何距离，马上就会走出三角形。

对上式稍微做一点变形，可以得到：

p−A=uAB→+vAC→pA→=uAB→+vAC→uAB→+vAC→−pA→=0p - A = u\overrightarrow{AB} + v\overrightarrow{AC} \\ \overrightarrow{pA} = u\overrightarrow{AB} + v\overrightarrow{AC} \\ u\overrightarrow{AB} + v\overrightarrow{AC} - \overrightarrow{pA} = {0}

可以这么理解这个式子：我们把包括 pp 点在内的所有点都通过 −OA→-\overrightarrow{OA} 移动了一个距离，这个时候 AA 一定在原点。

这样这个式子就很直观了：先通过 uAB→+vAC→u\overrightarrow{AB} + v\overrightarrow{AC} 这个向量从原点走到 pp 点，再从 pp 点用 pA→\overrightarrow{pA} 走回 AA，也就是原点。

因为这两个部分方向相反并且大小相同（一个从 AA 走到 pp，一个从 pp 走到 AA），所以这两个向量相加一定是 0。

拆开这个式子，再重新整理，可以得到：

u(B−A)+v(C−A)+A−p=0uB−uA+vC−vA+A−p=0A(1−u−v)+uB+vC−p=0(1−u−v)A+uB+vC=p\begin{align*} u(B - A) + v(C - A) + A - p &= 0 \\ uB - uA + vC - vA + A - p &= 0\\ A(1 - u - v) + uB + vC - p &= 0 \\ (1 - u - v)A + uB + vC &= p \end{align*}

这个形式完全和重心坐标一致，所以我们可以确定：α=1−u−v\alpha = 1 - u - v，β=u\beta = u，γ=v\gamma = v。

把这些东西相加，可以发现 1−u−v+u+v=11 - u - v + u + v = 1，确实，重心坐标的三个系数相加一定是 1。

前面我们已经说明了，uu 和 vv 是非负的，但如果 u+v>1u + v > 1，α\alpha 不就是负数了吗？

考虑下图，AMAM 是 AA 到 BCBC 的一条垂线（MM 不是 BCBC 的中点，这里不用等边三角形可能更清晰，但是我懒）：

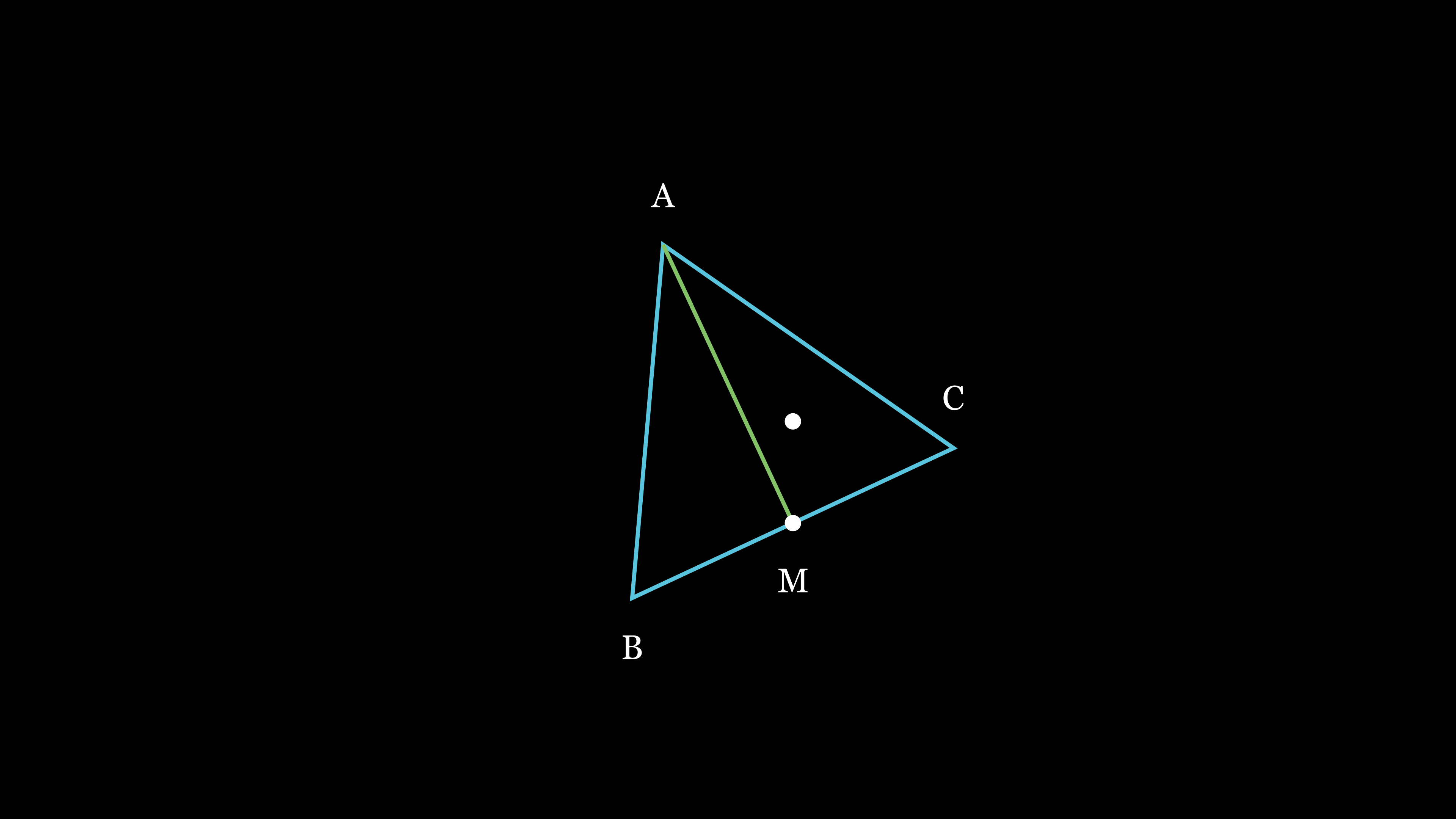
回到最初的定义中，也就是 p=A+uAB→+vAC→p = A + u\overrightarrow{AB} + v\overrightarrow{AC}，uvuv 分别是朝 AB→\overrightarrow{AB} 和 AC→\overrightarrow{AC} 方向走过的距离。

那么 uAB→u\overrightarrow{AB} 投影在 AM→\overrightarrow{AM} 上的长度就是 uAB→⋅AM→∣AM→∣u\overrightarrow{AB} \cdot \overrightarrow{AM} \over |\overrightarrow{AM}|

观察上图可以发现，如果 uu 为 1，也就是 AB→\overrightarrow{AB} 有完整的长度，这个投影的长度一定等于 ∣AM→∣|\overrightarrow{AM}|。同样的，如果 uu 为 0，投影在 AM→\overrightarrow{AM} 方向的长度也一定是 0。

因为投影，或者说点乘是一个线性的操作，所以如果 uu 为 0.5，投影的长度一定是 ∣AM→∣|\overrightarrow{AM}| 的一半。

因此我们可以说，AB→\overrightarrow{AB} 在 AM→\overrightarrow{AM} 上的投影长度是 u∣AM→∣u|\overrightarrow{AM}|

相同的，AC→\overrightarrow{AC} 在 AM→\overrightarrow{AM} 方向的投影长度符合一样的规则。

为了让 pp 点留在三角形内部，uAB→+vAC→u\overrightarrow{AB} + v\overrightarrow{AC} 这个向量投影在 AM→\overrightarrow{AM} 上的长度必须小于等于 AM→\overrightarrow{AM} 本身的长度，不然 pp 点就会从 BCBC 这条边跑出三角形。

AB→\overrightarrow{AB} 在 AM→\overrightarrow{AM} 上的投影长度是 u∣AM→∣u|\overrightarrow{AM}|，AC→\overrightarrow{AC} 在 AM→\overrightarrow{AM} 上的投影长度是 v∣AM→∣v|\overrightarrow{AM}|，自然，这两个向量的和在 AM→\overrightarrow{AM} 上的投影长度就是 (u+v)∣AM→∣(u + v)|\overrightarrow{AM}|。

前面说过，为了使得 pp 点留在三角形内部，uAB→+vAC→u\overrightarrow{AB} + v\overrightarrow{AC} 这个向量投影在 AM→\overrightarrow{AM} 上的长度必须小于等于 AM→\overrightarrow{AM} 本身的长度，也就是 (u+v)∣AM→∣≤∣AM→∣(u + v)|\overrightarrow{AM}| \le |\overrightarrow{AM}|，那么 u+v≤1u + v \le 1。

因为 α=1−u−v\alpha = 1 - u - v，并且 u+v≤1u + v \le 1，所以我们可以说明，α\alpha 也一定是非负的。

至此我们已经能说明，为什么一个在三角形内部的点就要符合 α+β+γ=1\alpha + \beta +\gamma = 1，并且每个系数非负了。当然要把一个平面直角的坐标转换到重心坐标，还是需要一些相对复杂的计算的。这部分的内容，我觉得这篇博客中介绍的第一种方法相对易于理解并且很巧妙，有兴趣的可以看下。