P8095 [USACO22JAN] Cereal 2 S题解

前言：题解可能比较啰嗦，因为这题比赛的时候没做出来，所以写题解主要用于整理自己的思路。如果你有思路只是代码打挂了简易直接跳到代码部分。

update@2022/3/13: 感谢@小木虫的提醒，当前的解法不是正解！ 如果USACO的数据够强的话，目前我使用的匈牙利算法因为复杂度是 $O(nm)$，是过不了这道题的。如果想用我这个二分图匹配 + 拓扑的方法实现，可以使用dinic算法求二分图最大匹配（不过写起来会比较麻烦）。本人有时间的时候也会尝试用dinic实现这个解法并且更新题解。

题目链接

博客中观看体验更佳

1：题意

有 $N$ 头牛，$M$ 种麦片（每种一箱），每头都有第一和第二喜欢的麦片种类（下文简称为一选和二选），牛会优先选择自己最喜欢的麦片，当最喜欢的麦片被占用后会选择第二喜欢的麦片，问：

1. 最少会有多少牛得不到麦片。
2. 能达到此最小值的牛的排列

2：分析

2.1 第一小问

对于第一个小问，可以发现这是一个标准的二分图最大匹配问题，很容易想到使用匈牙利算法解决（然而这次比赛的时候我并没有想到）。不熟悉匈牙利算法和二分图匹配问题的同学可以参考模板题里的题解。这篇题解将主要关注第二小问的求解。

2.2 第二小问

对于第二小问，我一开始想的是先输出成功匹配到一选的牛，其次是成功匹配到二选的牛，最后输出没有成功匹配的牛。结果交上去只过了样例。经过@lutongyu大佬的指导，我终于理解了这个做法的问题。

具体来说，对于成功匹配到一选的奶牛，可以先输出，最后输出没有成功匹配的奶牛也是没有问题的。真正的问题在于二选奶牛的顺序。考虑下面这样的一个数据（如下图）:

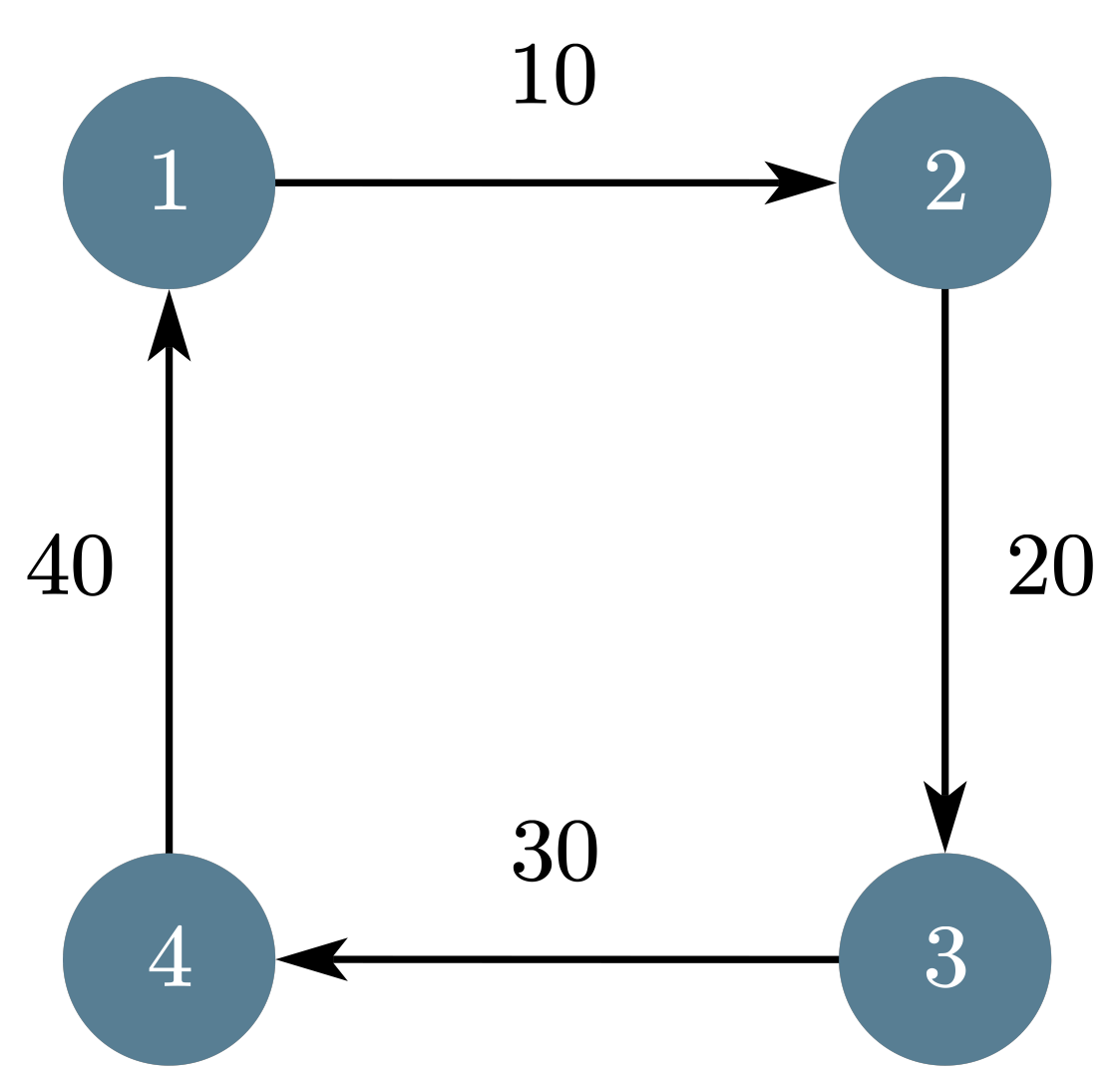
1 (cow) -> [1 (fir), 2 (sec)]
2 (cow) -> [1 (fir), 3 (sec)] 
3 (cow) -> [3 (fir), 4 (sec)] 

我们可以试着手动模拟一下这个数据

我们首先尝试这个数据下的最优排列 1 2 3

1. $\text{Cow}_1$ 会先选择它的一选，也就是麦片 1
2. 因为 $\text{Cow}_2$ 的一选被 $\text{Cow}_1$ 占用了，所以它会选择它的二选，也就是麦片 3
3. $\text{Cow}_3$ 的一选被 $\text{Cow}_2$ 占用了，所以它会选择他的二选，也就是麦片 4

在这样的情况下，每一头奶牛都能吃到麦片

然后我们调换一下 $\text{Cow}_2$ 和 $\text{Cow}_3$ 的顺序，得到1 3 2 的顺序，以及下面的模拟过程

1. $\text{Cow}_1$ 会选择它的一选，也就是麦片 1
2. $\text{Cow}_3$ 会选择它的一选，也就是麦片 3
3. $\text{Cow}_2$ 的一选和二选都被占用了（麦片 1 3），它不能吃到麦片

在这样的情况下，$\text{Cow}_2$ 并不能吃到任何麦片

通过这个数据，我们可以发现直接输出匹配到二选的牛是不行的，还需要在输出匹配到二选的牛时做一些处理，保证这个排列能达到最大匹配数。

具体来说，我们可以使用一种类似拓扑排序的算法来解决二选奶牛的冲突问题。

我们首先来考虑当一头奶牛成功匹配到自己的一选，并且它的一选同时也是别的奶牛的一选会发生什么，拿上图中的 $\text{Cow}_1$ 举例子，它会影响到 $\text{Cow}_2$ 的选择（$\text{Cow}_1$ 占用了 $\text{Cow}_2$ 的一选，迫使其选择二选），而 $\text{Cow}_2$ 又会影响到 $\text{Cow}_3$ 的选择（$\text{Cow}_2$ 占用了 $\text{Cow}_3$ 的一选，迫使其选择二选）。通过观察，我们可以发现只要按照这样一个 “影响链” 来输出奶牛，就可以保证达到最大匹配。

3：算法过程

这一条链的开始一定是成功匹配到一选，并且迫使别的奶牛选择二选的奶牛（这个奶牛的一选也是别的奶牛的一选）。我们把这样的奶牛全部入队。我们再来考虑被影响的奶牛，为了找出 “影响链” 我们需要把这些被影响到的奶牛也入队（因为这些奶牛只能选择二选，而他们的二选可能会占用别的奶牛的一选，就像上图中的 $\text{Cow}_2$）。

为了找出有哪些牛是可能被影响的，我们可以引入一个 inv_e[i] 的动态数组（链式前向星），表示所有把 i 号麦片作为一选的牛（只有一选先被别的牛选了才会被影响）。

比如在上图中 inv_e[1] = [ $\text{Cow}_1$ , $\text{Cow}_2$ ]

我们知道在实现匈牙利算法的时候会用到 matched[i] 数组。它的下标表示右部节点，值表示匹配到这个右部节点的左部节点。在这题中，matched[i] 的下标就是麦片的编号，而值是匹配到这个麦片的牛。我们可以引入一个 inv_match[i] 数组，它的下标是牛，而值是麦片。通过 inv_match 我们可以知道每头牛最终匹配到的麦片是哪个（一选二选或者匹配失败）。

用上图举例子， inv_match[ $\text{Cow}_2$ ] 就等于麦片 3 （最终匹配到的是麦片 3）

下面的代码展示了如何找到所有被一选奶牛所影响的奶牛

for(int i = 1; i <= n; i++){              //i遍历的是成功匹配到一选的奶牛
    if(invmatched[i] != e[i][0]) continue;//e[i][0]表示i的一选
                                          //invmatched[i] 是i最终匹配到的麦片
                                          //所以这句话的意思是如果不是一选就直接continue
    printf("%d\n",i);//如果是一选直接输出

    for(int cur:inve[e[i][0]]){         //遍历当前成功匹配一选的牛 可能影响的牛
                                        //e[i][0]表示的是i的一选，而i一定是成功匹配一选的牛
                                        //inve[e[i][0]]是所有一选和i的一选相同的奶牛，这些奶牛可能被i影响
        if(invmatched[cur] == e[cur][1])//前文提到了invmatched[cur] 表示的是cur最终匹配到的麦片
                                        //而e[cur][1] 表示的是 cur 的二选
        {                               //所以这句话确保了cur最终选到的是二选（说明这头牛被影响到了，没有选一选，同时也可以防止把i自己入队）
            q.push(cur);
        }
    }
}

接下来，对于已经进入队列的奶牛，他们的二选可能会占用别的奶牛的一选，所以我们也可以用相似的方法找出这个 “影响链”

while(!q.empty()){
    int cur = q.front();
    printf("%d\n",cur);//队列是先进先出的结构，所以可以先输出在影响链上方的牛（更早被影响到的牛）
    q.pop();
    for(int nex:inve[e[cur][1]]){         //e[cur][1]是编号为cur的牛的二选
                                          //inve[e[cur][1]] 就是所有把 cur 的二选当作一选的牛，也就是可能被 cur 影响到的牛
        if(invmatched[nex] == e[nex][1]) {//最终选到的是二选（说明这头牛被影响到了）
            q.push(nex);
        }
    }
}

4：代码实现以及细节

最后给出详细代码（有注释解释细节）

/*Date: 22 - 02-03 22 19
PROBLEM_NUM: P8095 [USACO22JAN] Cereal 2 S*/
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 10;
int n, m;
vector<int> e[MAXN], inve[MAXN];
queue<int> q;
int vised[MAXN], matched[MAXN];
int invmatched[MAXN];

bool found(int cur){//匈牙利算法
    for(int nex:e[cur]){
        if(vised[nex]) continue;
        vised[nex] = true;
        if(!matched[nex] || found(matched[nex])){
            matched[nex] = cur;
            invmatched[cur] = nex;
            vised[nex] = false;
            return true;
        }
    }
    return false;
}

int main(){
    int match_cnt = 0;
    scanf("%d%d",&n,&m);
    for(int i = 1; i<=n; i++){
        int f,s;
        scanf("%d%d",&f,&s);
        e[i].push_back(f);   //e[i][0]是i的一选
        e[i].push_back(s);   //e[i][1]是i的二选
        inve[f].push_back(i);//inve[f] 表示所有把 f 号麦片作为一选的牛
    }
    for(int i = 1;i <= n; i++){//匈牙利算法部分
        if(found(i)){
            match_cnt++;
        }
    }

    printf("%d\n", n - match_cnt);//饥饿的奶牛 = 所有奶牛 - 吃到麦片的奶牛

    for(int i = 1; i <= n; i++){          //i遍历的是成功匹配到一选的奶牛
    if(invmatched[i] != e[i][0]) continue;//如果不是一选就直接continue
    printf("%d\n",i);                     //如果是一选直接输出

    for(int cur:inve[e[i][0]]){         //遍历当前成功匹配一选的牛 可能影响的牛
                                        //e[i][0]表示的是i的一选，而i一定是成功匹配一选的牛
                                        //inve[e[i][0]]是所有一选和i的一选相同的奶牛，这些奶牛可能被i影响
        if(invmatched[cur] == e[cur][1])//前文提到了invmatched[cur] 表示的是cur最终匹配到的麦片
                                        //而e[cur][1] 表示的是 cur 的二选
            {                           //所以这句话确保了cur最终选到的是二选（说明这头牛被影响到了，没有选一选，同时也可以防止把i自己入队）
                q.push(cur);
            }
        }
    }
    
    while(!q.empty()){
        int cur = q.front();
        printf("%d\n",cur);//队列是先进先出的结构，所以可以先输出在影响链上方的牛（更早被影响到的牛）
        q.pop();
        for(int nex:inve[e[cur][1]]){         //e[cur][1]是编号为cur的牛的二选
                                              //inve[e[cur][1]] 就是所有把 cur 的二选当作一选的牛，也就是可能被 cur 影响到的牛
            if(invmatched[nex] == e[nex][1]) {//最终选到的是二选（说明这头牛被影响到了）
                q.push(nex);
            }
        }
    }

    for(int i = 1; i<=n; i++){//最后输出没有成功匹配到的奶牛
        if(!invmatched[i]){   //invmatched[i] == 0 说明奶牛 i 没有匹配到任何麦片
            printf("%d\n",i);
        }
    }

    system("pause");
}

最后，希望这篇题解能帮到你，如果还没看懂或者是发现了题解有问题都可以私信我或者在评论区指出，我会尽量回答或是解决问题。