1：题意简述

有 $N$ 个奶牛，奶牛 $i (1 \le N)$ 想访问奶牛 $a_i (a_i \ne i)$ 。如果 $a_i$ 已经离开去访问别的奶牛了，则 $i$ 不能成功访问 $a_i$ ，否则，这次成功访问可以增加 $v_i$ 次哞叫。现在让你找出可能的最大哞叫次数

2：分析

理解题目后，我们可以首先分析下样例，试试看找一些有用的信息。

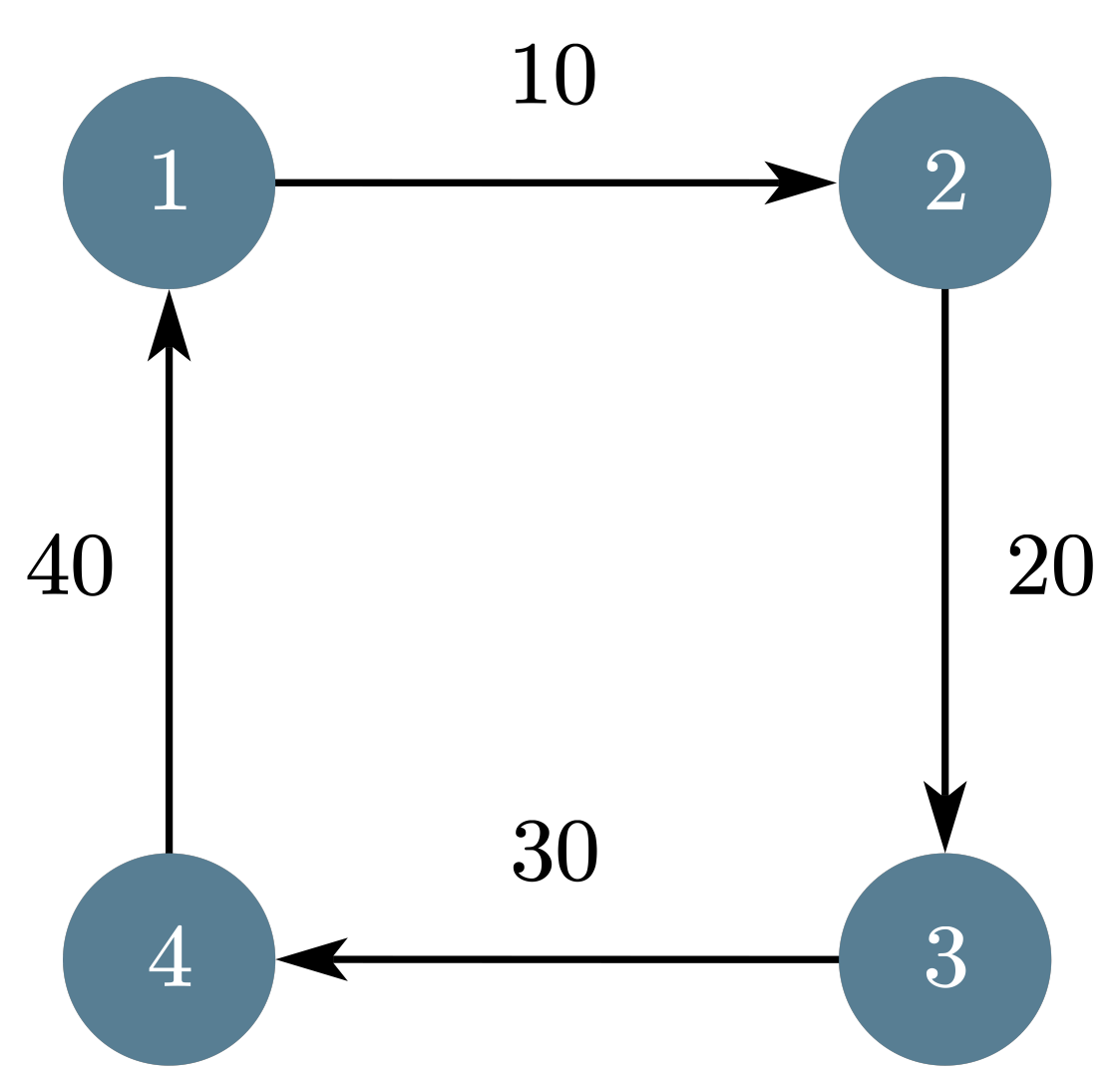
为了方便分析样例，我们可以把样例用图的形式展示，图中有向边连接的两个节点就是一头牛和这头牛希望访问的牛（ $i$ 和 $a_i$ )。而边权是这次访问能产生的哞叫次数。

通过这张图，我们可以发现，不管以什么样的顺序访问，最多都只能成功的访问三次，最后的一次访问一定会遇到之前已经遇到过的牛，所以选择 $2 \rarr 3$ ， $3 \rarr 4$ 和 $4 \rarr 1$ 可以达到最大的哞叫次数，也就是 $20 + 30 + 40 = 90$ 次。

再仔细思考这个样例，可以发现不能同时选四条边的本质原因是这样会在图中产生一个环。如果图中有环，并且必须要经过环上的每一条边，那么我们必然会访问到之前访问过的节点。

而如果我们能从原来的图中选出一些边，建出一个没有环的图，那么就一定能找出一种访问顺序，使得我们在遍历所有节点时不会重复访问节点。在不构成环的前提下，我们还需要尽量选择边权大的边，这样就能满足题目的要求——产生最多的哞叫次数。

没有环的，权值最大的图？好像跟最小（大）生成树很相似。

分析到这里，我们就比较容易想到使用最小（大）生成树算法了。通过这类算法，我们可以在图中找出权值最大的树。不过，这还是跟这道题不完全一样。我们还需要解决下面这个问题

最小（大）生成树的算法只能用于无向图中，而我们当前的图是有向图，所以我们可以直接把最小（大）生成树算法用在这道题里吗

（这部分如果理解了可以直接看代码)，代码就是个标准的 kruskal

换一种说法解释这个问题就是：从有向图转换来的无向图是否和原图等价？

比如上图这样的情况，不管使用什么访问顺序，三条边我们都是可以选的。但是转换成了无向图之后，就只能选择两条边了（选三条边会产生环）。

在题目中，每一奶牛只有一个想访问的奶牛，也就是说图中的每个节点出度都是 $1$ ，在这样的条件下，上图中的情况就是不可能出现的（上图中节点 $1$ 的出度为 $2$ ），并且转换出来的无向图和原图也是等价的。

那为什么只有入度大于 $1$ 时才会导致转换之后的无向图不等价于原来的有向图呢？

我们知道如果有 $n$ 个节点，要把这 $n$ 个节点包含在环中的最少边数是 $n$ 个。并且这 $n$ 个节点里面的每个节点的出度和入度都等于 $1$ 。就和样例中的一样。

一个边可以产生一个出度和一个入度。所以这个环里总共有 $2n$ 个度。如果我们允许一些节点的出度大于 $1$ ，那么有一些节点的入度可能是 $0$ 了（度的和一定为 $20$ ，那出度增加了入度就一定会减少），这样一来，入度为 $0$ 时没有别的节点能到达这个节点，自然就不能产生环。

但是如果把直接转换成无向图，出度和入度的总和还是 $2n$ ，每个节点的度也是 $2$ ，所以能构成环。

这样一来，在转换时就会产生问题了。

3：代码

这里我才用的是 Kruskal 来求的最大生成树，相较于这题的思维，代码还是比较简单的，只要把最小生成树中的排序改一下。

如果不熟悉最小生成树的算法，可以参考模板题里的题解

需要注意的是权值和可能会超过 int 的范围，需要开 long long。

/*Date: 22 - 03-26 15 28
PROBLEM_NUM: USACO MAR Problem 1. Visits*/
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 10;
#define ll long long
struct E
{
    int from, to, val;
} e[MAXN];
int n;
int fa[MAXN];
int find_fa(int cur)
{
    if (cur == fa[cur])
        return cur;
    return fa[cur] = find_fa(fa[cur]);
}
void merge(int a, int b)
{
    int af = find_fa(a), bf = find_fa(b);
    fa[af] = bf;
}
//并查集操作

ll ans;

int main()
{
    scanf("%d", &n);
    iota(fa + 1, fa + 1 + n, 1);//最开始 fa[i] = i
    for (int i = 1; i <= n; i++)
    {
        scanf("%d%d", &e[i].to, &e[i].val);
        e[i].from = i;
    }
    sort(e + 1, e + 1 + n, [](E a, E b)
         { return a.val > b.val; });//权值大的放前面
    int used_edge = 0;
    for (int i = 1; i <= n; i++)//kruskal
    {
        if (find_fa(e[i].from) != find_fa(e[i].to))
        {
            used_edge++;
            ans += e[i].val;
            merge(e[i].from, e[i].to);
            if (used_edge == n - 1)
            {
                break;
            }
        }
    }
    printf("%lld\n", ans);
    system("pause");
}