最近（距离搞完 RTOW 已经过去一周了，我现在才把这笔记写出来，属实是懒狗）花了一些时间看完了 Ray Tracing in One Weekend （以下简称 RTOW）果然还是我太菜了，这玩意 One Weekend 没搞完，也跟着把代码写出来了。

本书写的非常不错，最后渲染出的效果也是出乎我的意料（封面图）。但是因为我以前对计算机图形学没有任何的认识，很多基本的知识都不了解。

而书上有时会把这些基本知识（或者数学推导和证明）一笔带过，因此准备写个博客把自己的思考过程写一下。

朗伯体材质 （Lambertian） 的实现

在书中，创建一个朗伯体漫反射材质的方法是下面这样：

class lambertian : public material {
   public:
    lambertian(const color& alb) : albedo(alb) {}
    
    virtual optional<pair<ray, color>> 
    get_ray_out(const ray& r_in, const hit_rec& rec) const override {

        vec3 ref_dir = rec.norm + rand_unit_vec(); // 注意这里

        if(ref_dir.near_zero()) // 如果 rand_unit_vec() 等于 -rec.norm 
            ref_dir = rec.norm;

        ray ref_ray(rec.hit_pt, ref_dir);
        return make_pair(ref_ray, albedo);    
    }
    color albedo;  // 反射率
};

也就是，击中漫反射材质后，发散光线的起点（rec.hit_pt）会是击中的点，而发散光线的方向是一个随机的单位向量加上击中点的法向量。

但为什么要加上法向量呢，不能直接在一个半球形里随机一个向量吗？

辐射度量学

要回答这个问题，需要对辐射度量学（radiometry）有一些认识。下面首先介绍一下一些辐射度量学的基本单位。

在光线追踪中，我们希望考虑相机（或者人眼）接收到的光照，所以下面的解释会以相机的视角进行。

基本单位

首先需要考虑相机传感器接收的到底是什么物理量，显然，是能量，或者说是到达传感器上的光子数量，那么我们认为传感器接收到的物理量是辐射能量（radiant energy）用符号 QQ 表示，单位为焦耳。

不过能量并不能很好的反应一个物体的亮度。毕竟我们拿着相机拍同一个画面，曝光一分钟和 1100\frac{1}{100} 秒的效果肯定是不一样的。

虽然传感器最终接收的是能量，但只要我们拿着相机不同的曝光（积分），就可以一直得到更多的能量。

自然而然的，我们会想到，把得到的能量除以收集能量的时间，那就有了辐射通量（radiant flux）这个单位：

Φ=dQdt\Phi = \frac{\mathrm{d}Q}{\mathrm{d}t}

也就是传感器在单位时间内能收到的能量。

反过来，这也可以表述某个光源在单位时间内传输的能量。

不过这还是不能完全的表示物体的亮度。如果我们在相机中使用更大的传感器，那么单位时间内更大的传感器能接收到更多的能量。

我们在观测时用更大的传传感器并不能改变物体本身的亮度。因此还需要把接收到的辐射通量除以面积，也就是单位面积下的辐射通量。这个单位被称为辐照度（irradiance）。

对于光源来说，使用一个更大的光源，也能提供更多的辐射通量，但是单位面积能提供的通量是不变的。

E=dΦdAE = \frac{\rm{d}\Phi}{\rm{d}A}

考虑下面这样一张图[1]：

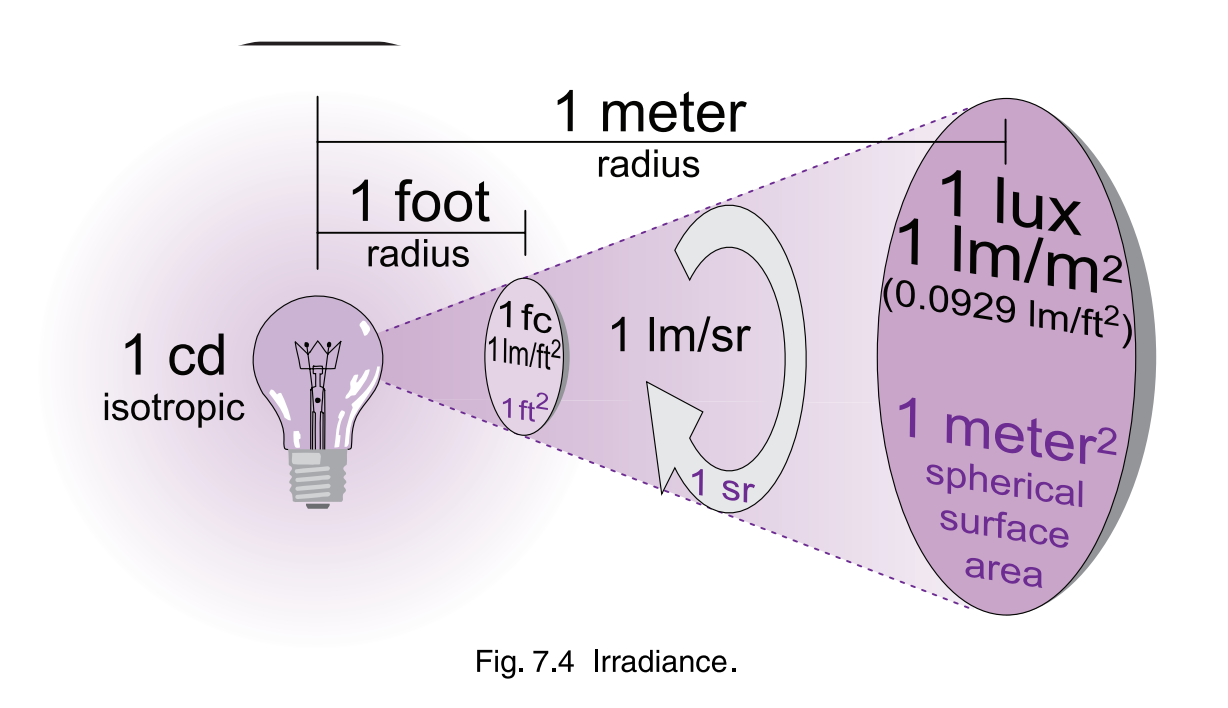
我们会发现，观测距离变远，要收集到相同的光通量，所需的面积就要越大。那么辐照度就会越小。这显然是不符合常理的，现实中随着距离变远，我们所观察到的亮度并不会显著的减小（有衰减主要还是因为光线在传播中会碰到很多细小的颗粒）。

那这是怎么一会事呢？直观上讲，虽然观测距离更远了，收到的光通量更少了，但是人眼看到的物体也变小了。

比如有一个面积很大的灯，以及一个面积很小的灯，如果它们两个发出的光通量相同，显然是面积小的灯更亮。

因此，人眼直接接收到的光通量小了，但是观测物体的面积也对应的小了，这两个变化相互抵消，会造成观测到的亮度不变。那么我们就需要引入一个物理量，描述人眼观测到的物体大小，随后把辐射照度除以这个量，就能真正的描述亮度。而这个量就是立体角。

我们可以把人眼的视线想象成一个球，这个球的球心是人眼，因此球面上的每个点到人眼的距离都是一样的。也因此，如果我们在这个球面上放置很多大小一样物体，因为他们到人眼的距离一样，人眼看起来的大小也是一样的。

那对于距离不同的物体，都可以将其投影到这个球上面，这样在球面上占的面积大，人眼看起来也就大。

从光源的角度来说，有时我们会希望关注光源对某个方向的影响（把那个方向照亮了多少，提供了多少的辐射通量），那么这个时候也可以引入立体角来分析。

所以立体角的定义就是，某个物体在单位球（半径为 1 ）上的投影面积。

立体角的计算方法如下，单位为球面度（steradian, sr）：

Ω=aR2\Omega = \frac{a}{R^2}

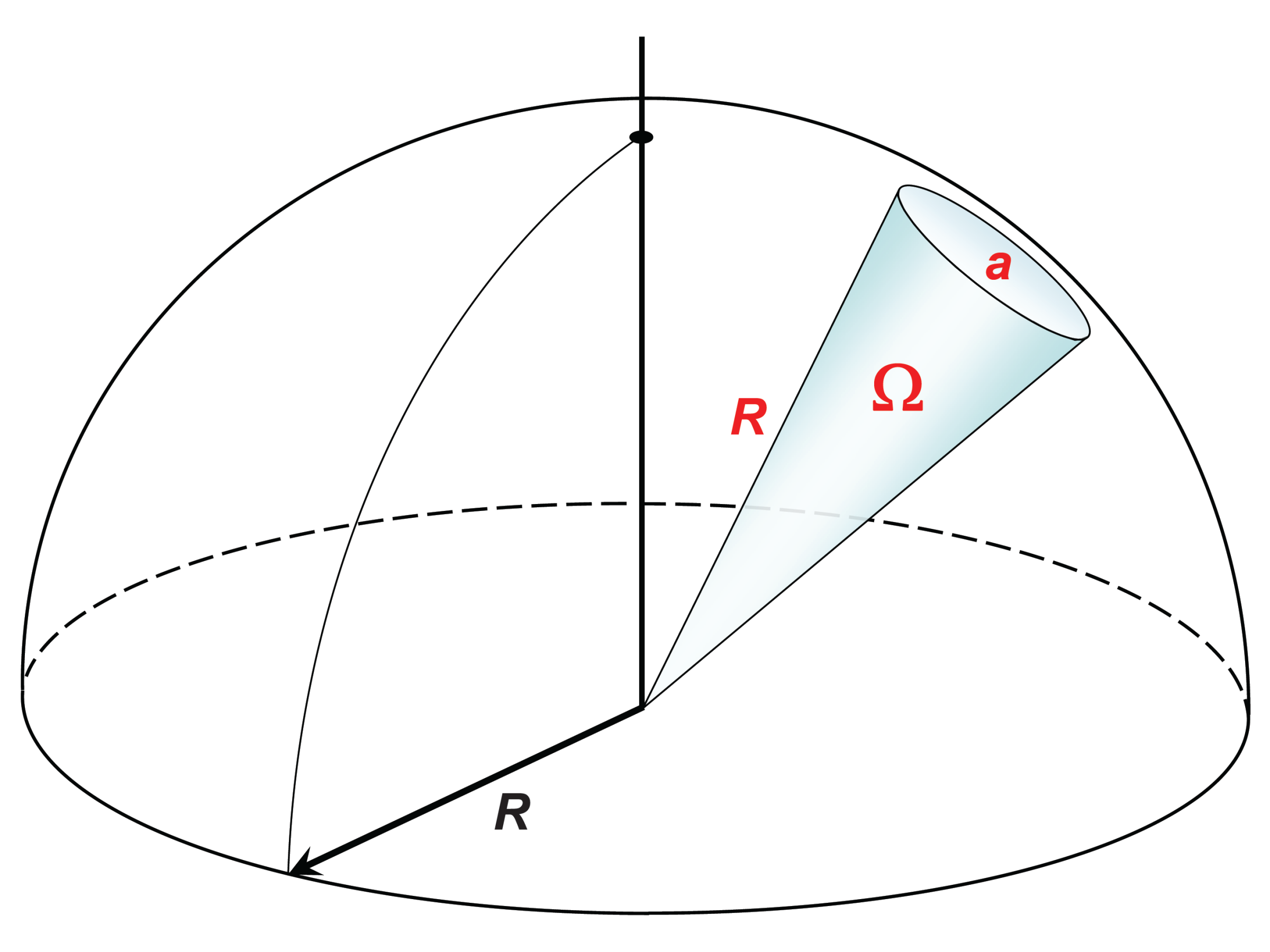
其中 aa 是投影在某个球上的面积（不一定是单位球），RR 是球半径。

那么有了立体角后，我们就能真实的描述人眼所看见的物体的大小了，进一步修改辐照度就可以得到辐亮度（radiance）这个物理量了：

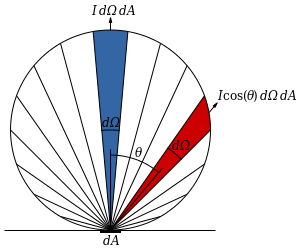
Lθ=dΦdAcos⁡(θ)dΩL_\theta = \frac{\rm{d} \Phi}{\rm{d}A\cos(\theta)\rm{d}\Omega}

这个公式中的 AA 是感光面元的面积，Ω\Omega 是球面度。而 cos⁡(θ)\cos(\theta) 其实是用来计算某个物体平行于球面的面积的，可以见下图：

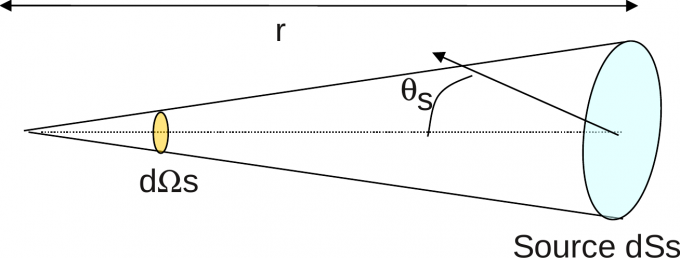
这里的 θ\theta 就是物体表面法线和球面法线的夹角，θ\theta 为 00 的时候 dAcos⁡(θ)\rm{d}A\cos(\theta) 最大，θ\theta 为 π2\frac{\pi}{2} 时，物体表面和球面垂直，因此球面发出的光线和物体完全不相交，dAcos⁡(θ)\rm{d} A \cos(\theta) 也就为 00。

辐亮度已经足够完美的描述大部分物体的亮度特征了。不过我们前面讨论的都是面光源，或者是有一定面积的传感器。一个点光源是没有面积的，这个时候辐亮度就没有意义了（因为要除以面积）。

同时，有的时候我们可能不关注光源和传感器的面积，单纯就是想知道某个发射或接收到的辐射通量，这个时候就需要有一种新的物理量——辐射强度（radiant intensity），它其实就是把辐亮度中除以面积的部分去掉了：

I=dΦdΩI = \frac{\rm{d}\Phi}{\rm{d}\Omega}

朗伯余弦定理

要理解朗伯余弦定律，可以看下面这张图：

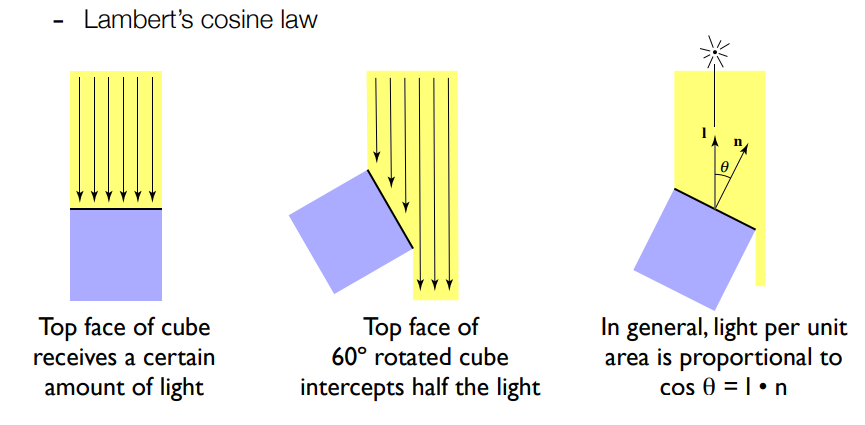
用数学公式表述的话就是：

Iθ=In×cos⁡θI_{\theta} = I_n \times \cos \theta

其中，InI_n 表示观察表面的法线完全平行于光线时的辐射强度。

对于观察者，θ\theta 是观察者表面的法线和光线的夹角，这个夹角越大，收到的辐射通量也就越小。而朗伯余弦定理选择的是辐射强度就是因为辐射强度规定了方向，这样就能计算出光线和表面法线的夹角（要不然光线可以从四面八方射过来）。

至于用的为什么是 cos⁡\cos，其实就是为了计算出当前观察表面投影到垂直于光线的表面后的面积。

朗伯体和漫反射

有了这些知识，就可以介绍朗伯体的性质了，以下是维基百科对朗伯体的介绍。

余弦辐射体，也称为朗伯辐射体（Lambert radiator），指的是发光强度的空间分布符合馀弦定律的发光体（不论是自发光或是反射光），其在不同角度的辐射强度会依馀弦公式变化，角度越大强度越弱

该规律以约翰·海因里希·朗伯的名字命名，因首次提出自他1760年出版的《光度学（Photometria）》。[2]遵循朗伯定律的表面被称为兰伯特表面，并表现出朗伯反射率。这样的表面从任何角度看都具有相同的辐射度。这意味着，例如，对人眼而言，它具有相同的视亮度（或亮度）。因为功率和实心角之间的比例是恒定的，所以辐射度（单位实心角单位投射源面积的功率）保持不变。

乍一看这两段话好像是反的。其中一个说强度符合照余弦定律，不同角度观察的强度不同，另一个亮度在任何角度都相同。

我们先根据定义分析一下，符合余弦定律也就是符合下面这个公式：

Iθ=In×cos⁡θI_{\theta} = I_n \times \cos \theta

回忆一下辐强度和辐亮度的定义：

Lθ=dΦdAcos⁡(θ)dΩL_\theta = \frac{\rm{d} \Phi}{\rm{d}A\cos(\theta)\rm{d}\Omega}

Iθ=dΦdΩcos⁡θI_{\theta} = \frac{\rm{d}\Phi}{\rm{d}\Omega} \cos \theta

尝试推导出 II 和 LL 的关系。

Lθ=Incos⁡θdAcos⁡θL_\theta = \frac{I_n \cancel{\cos \theta}}{\rm{d}A\cancel{\cos\theta}}

可以看到，分子和分母的 cos⁡θ\cos \theta 被消掉了，也就是角度对辐强度有影响，但是对辐亮度没影响。

直观上讲，这也是对的，我们从观察者的角度思考。如果 θ\theta 角大，那么观察者看到的发光表面是倾斜的，自然看到的面积也就小了。

虽然总体的辐射通量变少了，但是辐射通量从更集中的区域发出来，两者互相抵消，造成亮度没有变化（和介绍辐亮度时提到的很相）。

那么为什么发光表面在不同角度的辐强度不一样呢，假设发光表面每个区域的辐照度是一样的（单位面积的辐通量），θ\theta 角大的话，投影到观察者上的面积就小了，而这个投影面积的系数就是 cos⁡θ\cos \theta。

所以完美的漫反射体在不同角度看到亮度都是一样的。

所以，代码为什么这么写？

了解辐射度量学后我们就可以分析上面朗伯体的光线追踪代码了。

在光线追踪的时候，我们其实是在反方向（也就是从相机到光源）的追踪。但是对于一条从物体到相机的光线，可能有不同的光线对这条光线做出了贡献。

或者说，我们设物体上的点为 AA，而相机上的点是 BB，那么可能有很多条光线打到 AA 上，造成了 AA 最终的亮度和色彩。

所以在追踪时，光线从 AA 到达 BB 后，决定下一个追踪的方向就成了问题。

我个人认为，光线追踪时追踪的是辐射强度，也就是带方向的辐射通量。这是因为，相机传感器上每个像素（每个像素的面积一样，因此不用考虑面积）最后的颜色都取决于某个方向上的光通量。那么，不考虑面积，只有方向，就是辐射强度了。

这样在分析其他光线 BB 对点的贡献时，就要考虑朗伯余弦定理。

我们可以把 BB 点当作一个面积无限小的观察者，那么别的光线（单位辐射通量）和观察面的法线夹角越小，对该面贡献的也会按照 cos⁡θ\cos \theta 的系数衰减。

对于相机得到的每个像素点，我们都会进行多次采样，书里的代码如下：

……
color pixel_color(0, 0, 0);
for (int s = 0; s < samples_per_pixel; ++s) {
    auto u = (i + random_double()) / (image_width-1);
    auto v = (j + random_double()) / (image_height-1);
    ray r = cam.get_ray(u, v);
    pixel_color += ray_color(r, world);
}
write_color(std::cout, pixel_color, samples_per_pixel);
……

这样的多次采样可以模拟不同光线对 BB 点的贡献。为了模拟 cos⁡θ\cos \theta 的衰减，我们有两个选择，第一个是每次随机的选择一个 BB 点上单位半圆的表面作为光线的方向，继续追踪，大概和下图一样：

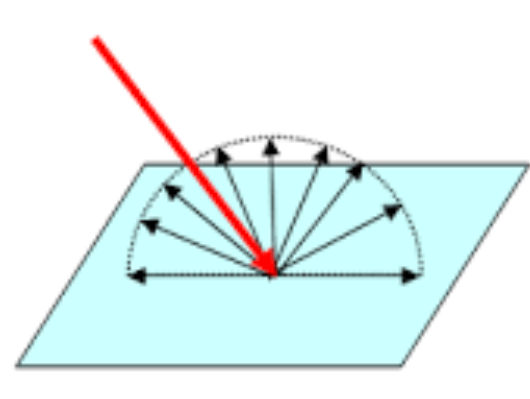
不过对于随机选出来的光线，需要计算其和 BB 点法线的夹角（θ\theta 角），然后加上衰减。

还有一种选择是，让 cos⁡θ\cos \theta 作为概率密度函数来随机的选取光线的方向，这样就不用加上衰减了，如下：

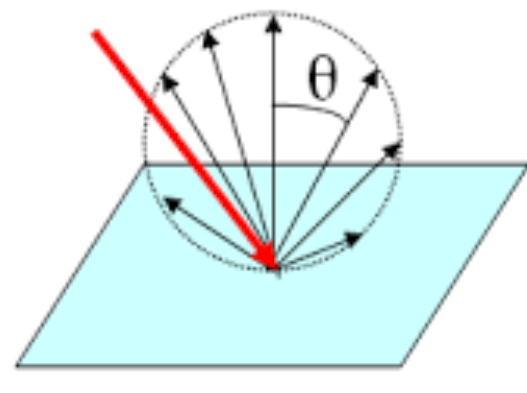
显然书里选择的是第二种方法，让 cos⁡θ\cos \theta 作为概率密度函数。这里有个比较神奇的事情，如果我们把 cos⁡θ\cos \theta 作为和 BB 的法线夹角为 θ\theta 的线段的长度，并把线段的一段固定在 BB 点上，就会得到下面的图像，即一个和 BB 点相切的圆，或者在三维空间里，球：

这里我暂时不知道如何证明，但这是一个正确的结论，如果你知道可以在评论区提出。RTOW 显然是利用了这一性质，让击中点的法向量加上一个随机的单位向量（单位球球面上的随机一点）作为光线的方向，如下：

vec3 ref_dir = rec.norm + rand_unit_vec();

这里还有个小问题，即为什么我们能保证，BB 点收到的光照就会向周围“均匀的”发散。前面我们说了，现在讨论的朗伯体的定义如下：

Iθ=In×cos⁡θI_{\theta} = I_n \times \cos \theta

我们追踪的也是辐射强度，那么不应该把表面的法线和摄像机的夹角算出来，然后加上 cos⁡θ\cos \theta 的衰减吗？

可以结合下面这张图理解：

可以观察到，随着夹角的增加，一个像素对应的物体表面积也相应的增大了，所以和 cos⁡θ\cos \theta 的衰减抵消了。

而对于每个像素，每次的采样是在一个像素的范围内任意选取坐标，所以可以覆盖到单个像素对应的物体表面。

如果真的要按照余弦定律加上衰减，我们也相应的对夹角更大的区域做更多的采样（单个像素对应的面积更大）。

参考资料：
1: https://www.cnblogs.com/ludwig1860/p/13930745.html
2: https://zh.wikipedia.org/zh-hans/余弦辐射体