Ray Tracing in One Weekend 学习笔记(2):相机类的实现
相机类的实现
除了朗伯体,RTOW 中还有个比较有趣的地方就是相机类的实现,特别是背景虚化这部分。
相机的定位
先来看一下相机类里一个相对简单的部分–相机的定位。只要通过三个参数就能确定相机的位置,分别是相机本身的位置(lookfrom),相机正在拍摄的位置(lookat)和表示相机上方位置的向量(vup),书里的图就能很好的解释:
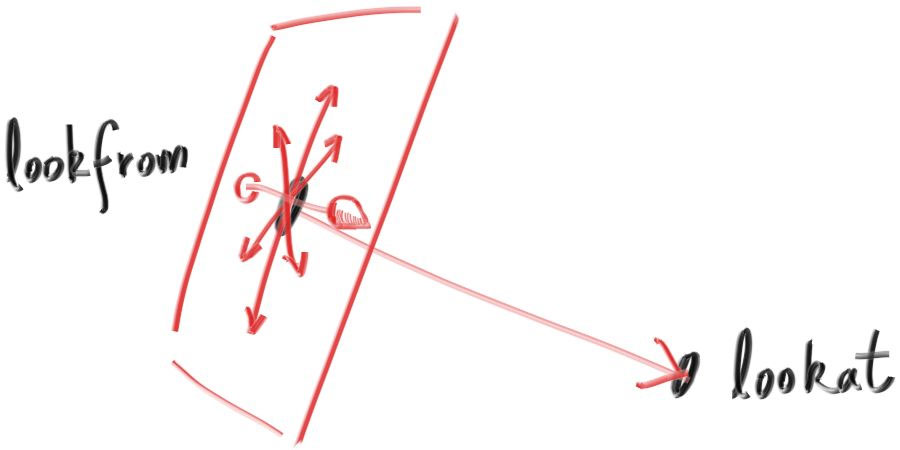
在构造函数中,我们需要把这三个参数转换成表示相机朝向的三个参数,以及做一些对焦距,光圈和 fov 的处理,书中没有在这部分花很多的篇幅,我当时想明白也花了挺久的,下面是我对书中实现的一些思考。
因为我对书中的代码稍作了一些修改(主要是命名?)所以先贴一下代码:
1 |
|
下面这张图描述了代码段中各个变量的关系:
按照这张图来理解代码中的内容就比较容易了。
下面这段代码首先计算出了两个变量 half_hei 和 half_wid:
1 | f8 deg_fov = deg2rad(vfov); |
其表示相机前方 1 个单位距离的位置上,看到的画面的大小。随后需要计算出 cam_x, y, z 三个向量,方法如下:
1 | cam_z = (lookfrom - lookat).unit_vec(); |
cam_z表示一个从lookat到loofrom的方向,这个方向和相机实际拍摄的位置是相反的。cam_x的计算用到了向量的叉乘,在三维空间中,如果 那么 就是同时垂直于 和 的,当然符合这个条件的向量有两个,可以用右手定则确定,这里就不赘述了。根据前面的这个定义,可以得出cam_x同时和cam_z和vup(也就是cam_z) 垂直。cam_y就是vup的单位向量。
虽然我大概知道三维向量叉乘的几何意义,不过以前没完全理解是如何推导出来的,感觉下面这篇博客写还是非常清晰的,连我这种蒟蒻也看懂了:
https://www.cnblogs.com/qilinzi/archive/2013/05/09/3068158.html
接下来 horizon,vertic 以及 lower_left_corner 变量的计算相对比较简单,这里就不解释了,图中都有标注。
相机景深的实现
现实中的景深
要理解计算机是如何模拟实现景深效果,还是需要对相机镜头的结构有一定基本的了解,如下:
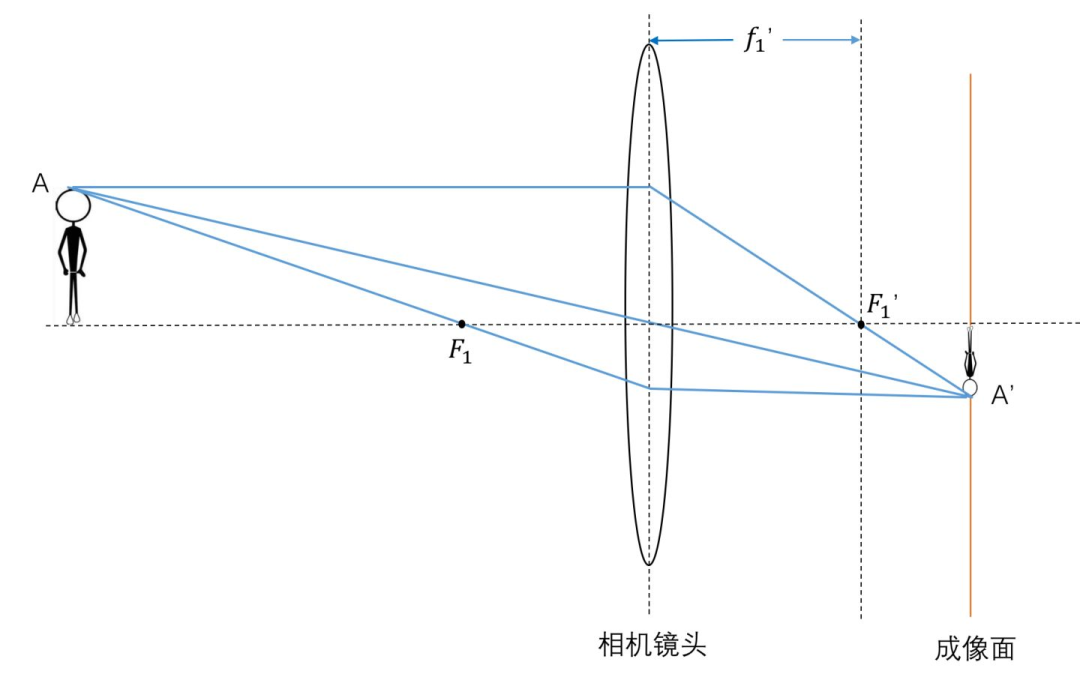
可以发现,在没有镜头的情况下,从 A 点出发的光线可以通过各种方向传播,每个方向又会到达成像面的不同位置。最终,成像面上每个点的颜色会由很多不同的光线贡献,得到的自然是模糊的影像。
加上镜头后再考虑 A 点,能观察到,从 A 点出发的每个方向的光线,最终都会汇聚在成像面的一个特定点上,也就是 A’。这样得到的影像就是清晰的了。
更宽泛的说,镜头能满足以下两个条件:
- 同一点发出的各个方向的光线,经过镜头后必定汇聚于同一点
- 同一平面上的不同点发出的光线,经过镜头后,汇聚于不同点
这里有一个前提条件,就是这个点必须在相机的焦平面上,如果某个点和相机成像面的距离不是焦距,就会有下面的情况:
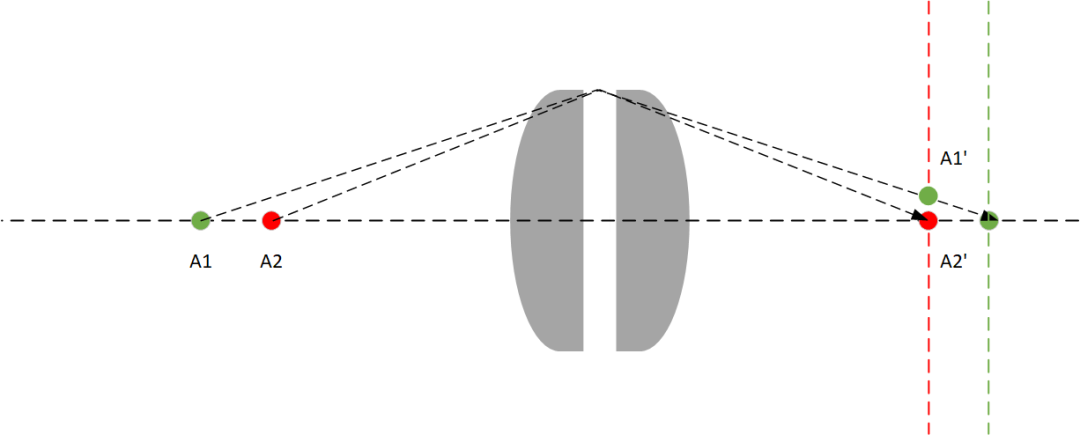
如果成像平面是绿色的那个,那么 A1 就在正确的焦平面上。如果成像平面是红色的那个,那么 A2 就在正确的焦平面上。
为了方便分析,我们观察 A1 的情况,发现在红色的成像平面上,从两个方向(平着和斜着)出发的光线被汇聚到了不同的点。而在绿色成像面上,只被汇聚到了一个点。
虽然被汇聚到了不同的点,但是这个不同的程度有大有小,可以想象一下,如果我们把 A1 的位置继续向左移动。那么 A1’ 在红色成像面的位置一定会更高。反过来,如果把 A1 向右移动,A1’ 在红色成像面的位置也会随之下降,最终汇聚在正确的点上。如果继续向右移动,A1’ 在红色成像面的位置还会继续下降。最终造成从 A1 平着出发的光线和斜着出发的光线,在成像面的距离增大。
或者我们增大镜头的尺寸,就有更多从 A1 出发的,不同角度的光线可以进入镜头中,进而到达成像面。这种情况下,A1’ 在红色成像面的位置会更高,可以想象镜头被拉高了,这里光线构成的三角形也被拉高了(我实在是懒的自己画图了,就用网上的图这么解释一下吧)。
看前面的图可以发现,理论上能被相机清晰成像的距离只有一个,多一点少一点都不清晰了。但实际上,人眼的分辨能力没有这么强。我们把相机成像时,能清晰成像(人眼认为是清晰的)的距离范围称作景深。如下:
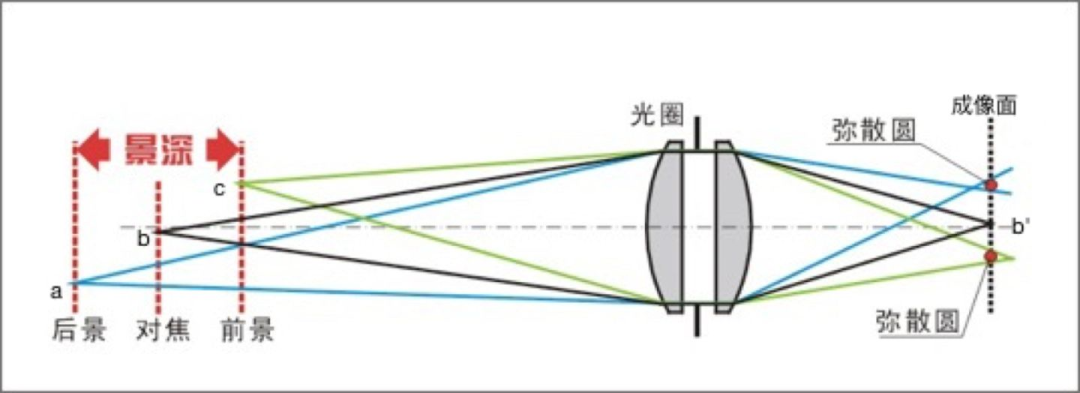
我们可以以景深的角度来思考前面提到的,镜头大小,或者说半径的影响。实际上,镜头的半径是不会改变的,通常的做法是给镜头加上一个可变的“闸门”,也就是光圈,来控制进入镜头的光线,如下:
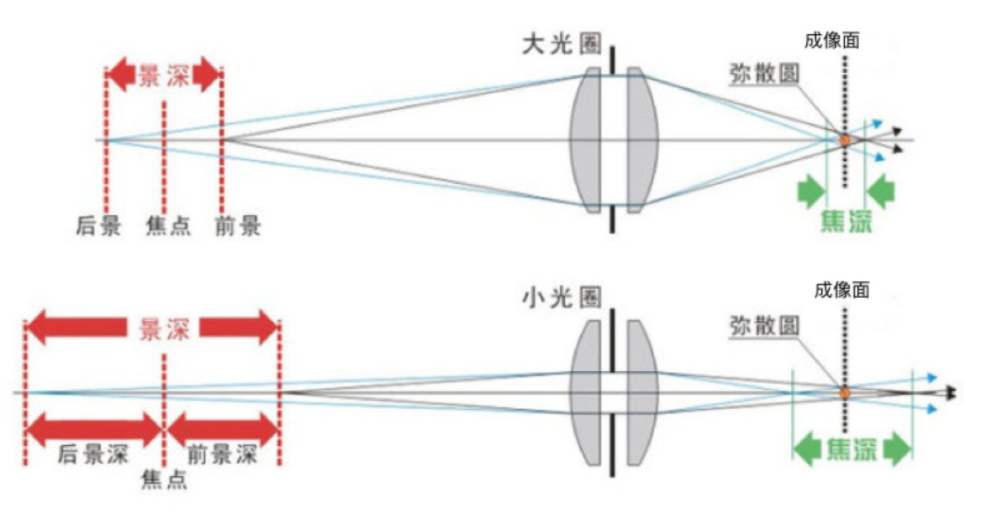
可以发现,大光圈会让景深减少,反之亦然。
实际实现
前面考虑过,从一个点出发的不同光线在不正确的焦距会被汇聚在成像面的不同点上。不过在实际渲染的时候,我们考虑的是不同的光线对于成像面某个像素的贡献。
那么在光圈大的时候,理应有更多方向的光线同时对成像面上一个点做出贡献,造成模糊的效果。具体可以见下图,也就是 RTOW 中对景深的实现:
代码中我们会随机的在光圈上取点,然后追踪从光圈到焦平面上对应像素的光线。最后把采样光线的贡献平均一下。这样光圈越大,景深也就越小。并且因为任何的光线都需要穿过焦平面上对应的点,所以可以确保焦平面上一定是清晰的。
对比上面实际镜头的工作原理还是非常不同的,但是达到了相同的效果。不过这也是因为光线追踪的特点,及从像素开始 “逆向” 的追踪。所以我们不关注实际镜头中,一个点发出的光线会被汇聚在成像面不同位置的问题。而换了一个角度思考,及有多少不同点发出的光线会对一个像素造成影响。不得不说书里的这个实现真的牛皮。
参考资料:







![[Stanford CS144] Lab4 实验记录](/img/CS144/tcp%E7%8A%B6%E6%80%81%E6%B5%81%E8%BD%AC%E5%9B%BE.jpg)
![[Stanford CS144] Lab0-Lab3 实验记录](/img/CS144/sponge%E7%BB%93%E6%9E%84%E5%9B%BE.svg)