一个多月终于断断续续搞完了第二本书里的内容。和前面两篇文章一样,这篇也会写一些我个人花了较长时间才搞懂的部分,以及一些我在原书基础上加的新功能。
对于原书就有的功能,会直接使用书上的代码,如果是我新加进去的功能,会使用自己的代码。因为我的代码在原书基础上做了较大幅度的变化(即使是原来就有的功能),所以只看一段代码可能不太明白,这里可以参考我的 GitHub 仓库: https://github.com/ttzytt/RTOW
bvh_node
这部分主要是一些小细节我当时没太理解。首先是
1 2 3 4 bvh_node::bvh_node ( std::vector<shared_ptr<hittable>>& src_objects, size_t start, size_t end, double time0, double time1 )
首先是这个构造函数的范围问题。每颗子树是不负责 end 位置的 hittable 的。也就是这个构造函数负责的是 [start, end) 这样的一个区间。
这也解释了代码中 sort 的用法:
1 std::sort (objects.begin () + start, objects.begin () + end, comparator);
std::sort() 会排序的其实是 [) 这样的一个区间(我之前居然没注意到这个 )。所以这里的 objects.begin() + end 其实没有包括 end。
在排序 vector 等容器时,使用的方法是 sort(vec.begin(), vec.end()) 乍一看没有把 .end() 位置的元素包含进去,但其实 .end() 指向的是一个空的,或者说是最后一个元素更后面的位置(这我之前也没注意到 ),所以用这样的方法可以把整个 vector 都排一遍序。
球面纹理坐标
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class sphere : public hittable { ... private : static void get_sphere_uv (const point3& p, double & u, double & v) auto theta = acos (-p.y ()); auto phi = atan2 (-p.z (), p.x ()) + pi; u = phi / (2 *pi); v = theta / pi; } };
这里使用了一个 atan2 的函数,而不是普通的 atan 函数。我们知道 tan 这个三角函数会返回圆对应角度的切线的斜率。那 atan 就是返回某个斜率的对应角度。但是我们在求纹理坐标时实际上希望从圆上的某个坐标得到对应的角度,当然可以直接使用 atan(y/x) 来先求斜率再求角度。
但问题就出在描述圆的是一个方程而不是函数,一个 x 坐标可能对应多个 y 坐标。那么一个斜率就可能对应多个角度。具体来说,虽然 ( x , y ) (x, y) ( x , y ) ( − x , − y ) (-x, -y) ( − x , − y ) atan 的话还需要自己再判断一遍坐标的符号,而 atan2 相当于做了这个工作。
棋盘格纹理
书中的实现
1 2 3 4 5 6 7 virtual color value (double u, double v, const point3& p) const override auto sines = sin (10 *p.x ())*sin (10 *p.y ())*sin (10 *p.z ()); if (sines < 0 ) return odd->value (u, v, p); else return even->value (u, v, p); }
这段代码把三个份量上的值加上 π \pi π
加入另一个轴后,因为 sin ( ) \sin() sin ( )
不过说实话我认为周期性的函数也不止三角函数这一种。书中这么写只是为了获得正负号,而不是具体的值,使用 sin \sin sin
一个很简单的例子就是让 x x x 100 100 100 50 50 50
y = mod ( x , 100 ) − 50 y=\operatorname{mod}\left(x,100\right)-50
y = mod ( x , 100 ) − 50
仅在表面的棋盘格
不难发现书中的棋盘格是基于点在空间中的绝对坐标的。所以才会出现上图那样的分层。既然我们已经可以计算球面的纹理坐标了(其他 hittable 的纹理坐标在书中也有讲,比如长方形片),其实可以做一个基于物体表面的棋盘格纹理,如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class surface_checker : public texture { public : using text_array = std::vector<std::shared_ptr<texture>>; surface_checker () = default ; surface_checker (const text_array& _texts, const std::pair<f8, f8> _siz = {514 , 114 }) : texts (_texts), polar_azim_siz (_siz) {} virtual color value (f8 polar, f8 azim, const pt3& p) const override int x_idx = (i8)(azim * polar_azim_siz.first); int y_idx = (i8)(polar * polar_azim_siz.second / 2.0 ); return texts[(x_idx + y_idx) % texts.size ()]->value (polar, azim, p); } text_array texts; std::pair<f8, f8> polar_azim_siz; };
这里的 text_array 允许了棋盘中有多于两种颜色,而 (azim * polar_azim_siz.first) 会把原本 [ 0 , 1 ] [0, 1] [ 0 , 1 ] polar_azim_siz.first,确保球上有 polar_azim_siz 的颜色变化。最后就可以得到如下的效果:
生成该场景的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 scene surf_check_sc () { hittable_list world; auto checker1 = make_shared <surface_checker>( surface_checker::text_array{ make_shared <fixed_color>(color (0.2 , 0.3 , 0.1 )), make_shared <fixed_color>(color (0.9 , 0.9 , 0.9 )), make_shared <fixed_color>(color (0.3 , 0.2 , 0.15 )), make_shared <fixed_color>(color (0.15 , 0.3 , 0.9 ))}, std::pair<f8, f8>{60 , 60 }); auto checker2 = make_shared <surface_checker>( surface_checker::text_array{ make_shared <fixed_color>(color (0.2 , 0.3 , 0.1 )), make_shared <fixed_color>(color (0.9 , 0.9 , 0.9 )), }, std::pair<f8, f8>{30 , 30 }); world.add (make_shared <sphere>(pt3 (0 , -10 , 0 ), 10 , make_shared <lambertian>(checker1))); world.add (make_shared <sphere>(pt3 (0 , 10 , 0 ), 10 , make_shared <lambertian>(checker2))); f8 asp_ratio = 1.0 ; vec3 lookfrom = pt3 (13 , 2 , 3 ) * 2 ; vec3 lookat = pt3 (0 , 0 , 0 ); f8 vfov = 40.0 ; auto dist_to_focus = 10.0 ; auto aperture = 0 ; vec3 vup (0 , 1 , 0 ) ; auto cam_ptr = make_shared <camera>(lookfrom, lookat, vup, vfov, asp_ratio, aperture, dist_to_focus, aperture, 1.0 ); return scene (make_shared <bvh_node>(world), blue_sky_back_ptr, cam_ptr); }
柏林噪声
柏林噪声是书中一个比较难理解的点,不过柏林噪声是基于普通的值噪声的。值噪声其实就是在空间中的整数坐标上随机的生成一些随机数,再利用这些整数的坐标来给别的坐标线性插值(线性插值不懂的可以见这个链接 ,个人认为讲的很清楚)。
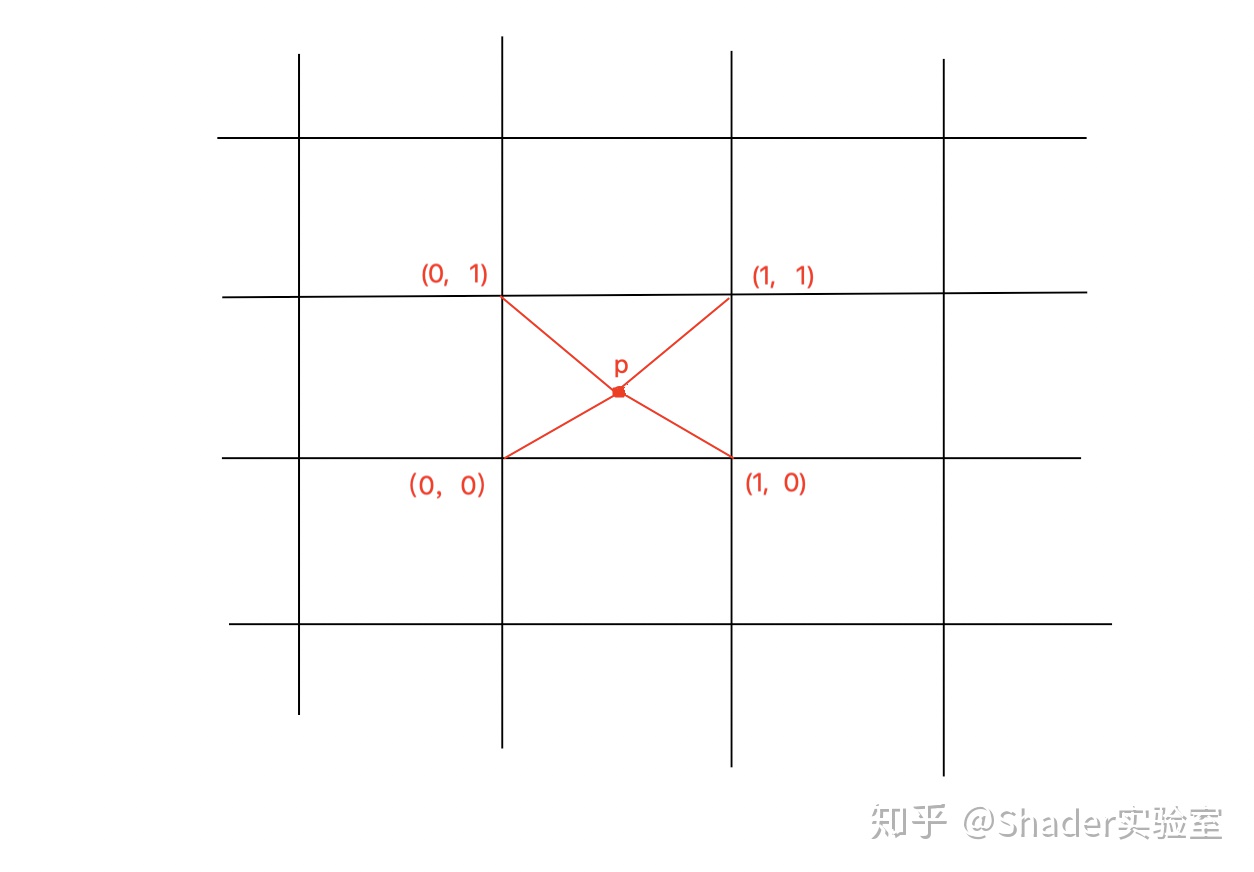
大概就是下面这样的[1]
垂直和平行线交错(整数坐标)的点会随机的生成一个随机数,而图中的 p 点会基于周围四个关键点(也就是坐标为整数的点,这些点会产生随机数)做线性插值,最终 p 点的值取决于离周围四个关键点的距离和周围四个关键点的随机值。
下面就是一个二维值噪声的例子:
生成代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 import numpy as npimport matplotlib.pyplot as pltfrom math import *XLEN = 25 YLEN = 25 DIFF = 0.05 ptsx = np.arange(0 , XLEN, DIFF) ptsy = np.arange(0 , YLEN, DIFF) xs, ys = np.meshgrid(ptsx, ptsy) z_orig = np.random.random((XLEN + 1 , YLEN + 1 )) z_interped = np.zeros((round ((XLEN) / DIFF), round (YLEN / DIFF))) def lerp (a, b, t ): return a + t * (b - a) def lerp2 (ld, rd, lu, ru, tx, ty ): upmid = lerp(lu, ru, tx) dnmid = lerp(ld, rd, tx) return lerp(dnmid, upmid, ty) for i in range (XLEN): for si in range (round (1 / DIFF)): for j in range (YLEN): for sj in range (round (1 / DIFF)): z_interped[i * round (1 / DIFF) + si][j * round (1 / DIFF) + sj] = lerp2( z_orig[i][j], z_orig[i + 1 ][j], z_orig[i][j + 1 ], z_orig[i + 1 ][j + 1 ], DIFF * si, DIFF * sj) plt.imshow(z_interped, cmap=plt.cm.gray) plt.savefig("./2d.png" , dpi = 150 , format = 'png' ) plt.show()
很容易看出这种噪声不自然,你甚至可以从图中隐约的看出坐标轴。。。虽然整张图看起来比较随机,但仔细观察就能发现整张图都是由很多小的 “方形色块” 拼凑而成的。
这是因为每个关键点对于各个方向的影响是相同的,而线性插值会让这个影响变成类似菱形的形状。下图中中间的点就是一个关键点,这个点随机出来的值比较低,所以是黑色的,可以看出这个黑色向周围发散的形状是菱形。
要改变这种情况也很简单,让某个关键点对周围的影响在不同的方向上不同。既然需要表示方向,我们可以很自然的想到向量。
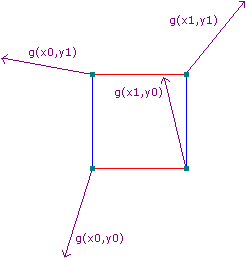
现在我们在每个关键点上产生一些随机的单位向量,记为 g i ⃗ \vec{g_i} g i i i i [2]
现在如何使用这些随机向量来达成不同方向影响就成了一个问题。一个比较自然的想法是考虑某个点相对于关键点的位置。我们可以把这个距离向量标记为 d i ⃗ \vec{d_i} d i i i i [2]
如果 d i ⃗ \vec{d_i} d i g i ⃗ \vec{g_i} g i d i ⃗ \vec{d_i} d i g i ⃗ \vec{g_i} g i
这样的效果可以通过点积来达到,其实就是把 d i ⃗ \vec{d_i} d i g i ⃗ \vec{g_i} g i
我们把这个点乘记录下来:
v i ⃗ = d i ⃗ ⋅ g i ⃗ \vec{v_i} = \vec{d_i} \cdot \vec{g_i}
v i = d i ⋅ g i
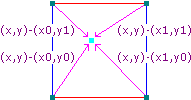
接下来就可以用值噪声的方式对周围四个点做线性插值了。或者说我们把 v i ⃗ \vec{v_i} v i
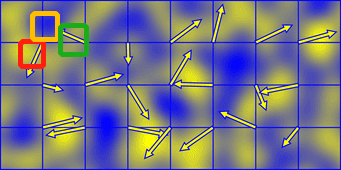
下面这张图展示了柏林噪声的效果,其中不同的箭头代表不同的 g i ⃗ \vec{g_i} g i [2]
注意看图中的三个框。
红框中大部分是黄色的,因为这部分点的距离向量和关键点的随机向量有相似的方向。
黄框中大部分是蓝色的,因为其左下角关键点随机向量的尾部指向了这片区域,也就是这片区域的距离向量和关键点随机向量相反。
绿框中的大部分是黄色的,虽然这片区域是左边关键点随机向量的反方向,但因为线性插值的存在,并且这片区域离右边的随机向量更近,其受到右边随机向量的影响更大。
可以很明显的看出,柏林噪声的生成的噪声并没有值噪声的方块感。
湍流(turbulence)
观察下面实现湍流的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 double turb (const point3& p, int depth=7 ) const auto accum = 0.0 ; auto temp_p = p; auto weight = 1.0 ; for (int i = 0 ; i < depth; i++) { accum += weight*noise (temp_p); weight *= 0.5 ; temp_p *= 2 ; } return fabs (accum); }
其中 turb 这个函数自身比较好理解,就是把很多频率的柏林噪声以一定的权重叠加在一起。最后的 fabs 看起来是为了让返回值符合 [ 0 , 1 ] [0, 1] [ 0 , 1 ] return (accum + 1) * 0.5,虽然让返回值符合了范围,但是看起来的效果却和原写法非常不同。
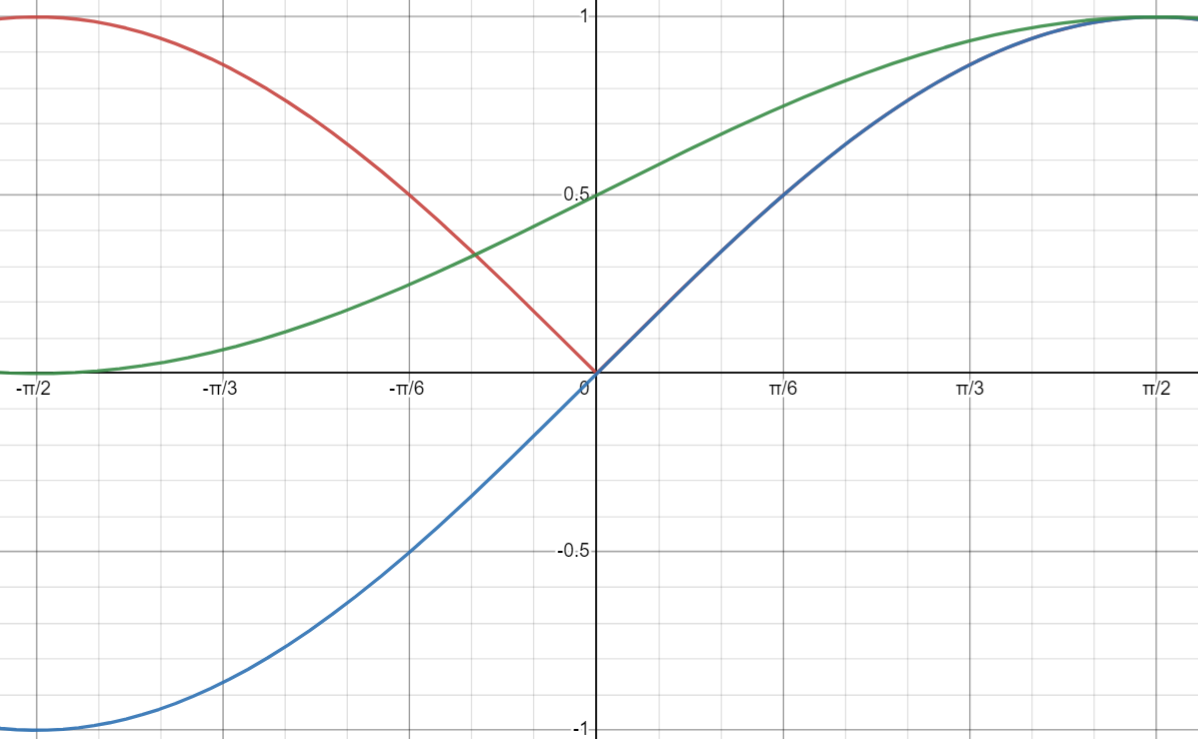
下图是中的蓝线是 y = sin x y = \sin x y = sin x y = ∣ sin x ∣ y = |\sin x| y = ∣ sin x ∣ y = ( sin ( x ) + 1 ) × 0.5 y = \left(\sin\left(x\right)+1\right)\times 0.5 y = ( sin ( x ) + 1 ) × 0.5
如果采用绿线的修正方法,原来暗的地方修正过后还是暗,反之亦然。如果采用红线的修正方式,则只有原本亮度中等或者说明暗过度的地方会变暗,不管是暗部还是亮部在修正过后都会变亮。对比书中两种材质的一个特征区域可以更明显的看出红色修正方式的特点:
左图的黑边像是给右图的黑色区域描了一个边,符合刚刚只有过渡部分会变暗的预测。
一些疑问
代码中的 noise(p) 返回的最大值是 1,而 weight 最开始的值也是 1。这样的话 abs(accum) 是有可能大于 1 的。这显然是没道理的,因为不可能光线打到某个物体后还变亮(除光源)了。我之前给这个博客 的博主发过这个问题有关的邮件,不过他表示他也不知道,可能只是概率问题使得大于 1 的值很少见。
随后我又查看了 Ken Perlin 1985 年在 SIGGRAPH 上的论文[3]
Noise()Noise() is a scalar valued function which takes a three dimensional vector as its argument. It has the following properties :
Statistical invariance under rotation (no matter how we rotate its domain, it has the same statistical character)
A narrow bandpass limit in frequency (its has no visible features larger or smaller than within a certain narrow size range)
Appendix. Turbulence
1 2 3 4 5 6 7 function turbulence(p) t = 0 scale = 1 while (scale > pixelsize) t += abs(Noise(p / scale) * scale) scale /= 2 return t
扰动的伪代码和书中的基本没有区别,但是对于 Noise() 函数 Perlin 只说了其接收一个点的位置,返回一个标量,没有标量的范围,所以还是比较令人疑惑的。
但是下文的一句话还是令人感觉他是想返回一个 [ 0 , 1 ] [0, 1] [ 0 , 1 ] [ 1 , 1 , 1 ] [1, 1, 1] [ 1 , 1 , 1 ]
By evaluating Noise() at visible surface points of simulated objects we may create a simple “random” surface texture (figure Spotted.Donut) :color = white * Noise(point)
这个问题实在是困扰了我比较久,如果你知道正确的解释是什么,欢迎在评论区提出,我过一段时间也准备去 stackoverflow 提个问,如果有结果我会更新这篇博客。
实例变换
旋转矩阵
公式推导
最初看到书中下面几个公式的时候我是比较懵逼的:
x ′ = cos ( θ ) − sin ( θ ) ⋅ y y ′ = sin ( θ ) + cos ( θ ) ⋅ y x^\prime = \cos(\theta) - \sin(\theta) \cdot y \\
y^\prime = \sin(\theta) + \cos(\theta) \cdot y
x ′ = cos ( θ ) − sin ( θ ) ⋅ y y ′ = sin ( θ ) + cos ( θ ) ⋅ y
上网找了一圈后发现其实是旋转矩阵,公式的推导如下(前面这个公式是绕 z 轴旋转的,我们可以简单理解为二维平面上的旋转矩阵)[4]
我们先把 x x x y y y
x = r cos ϕ y = r sin ϕ x = r\cos\phi \\
y = r\sin\phi
x = r cos ϕ y = r sin ϕ
在原来的角度上加上 θ \theta θ
x ′ = r cos ( ϕ + θ ) y ′ = r sin ( ϕ + θ ) x^\prime = r\cos(\phi + \theta) \\
y^\prime = r\sin(\phi + \theta)
x ′ = r cos ( ϕ + θ ) y ′ = r sin ( ϕ + θ )
使用如下两个两角和差公式:
cos ( ϕ + θ ) = cos ϕ cos θ − sin ϕ sin θ sin ( ϕ + θ ) = sin ϕ cos θ + cos ϕ sin θ \cos(\phi + \theta) = \cos\phi\cos\theta - \sin\phi\sin\theta \\
\sin(\phi + \theta) = \sin\phi\cos\theta + \cos\phi\sin\theta
cos ( ϕ + θ ) = cos ϕ cos θ − sin ϕ sin θ sin ( ϕ + θ ) = sin ϕ cos θ + cos ϕ sin θ
带入 ( x ′ , y ′ ) (x^\prime, y^\prime) ( x ′ , y ′ )
x ′ = r ( cos ϕ cos θ − sin ϕ sin θ ) x ′ = ( r cos ϕ ) cos θ − ( r sin ϕ ) sin θ x ′ = x cos θ − y sin θ \begin{align*}
x^\prime &= r(\cos\phi\cos\theta - \sin\phi\sin\theta) \\
x^\prime &= (r\cos\phi)\cos\theta - (r\sin\phi)\sin\theta \\
x^\prime &= x\cos\theta - y\sin\theta
\end{align*}
x ′ x ′ x ′ = r ( cos ϕ cos θ − sin ϕ sin θ ) = ( r cos ϕ ) cos θ − ( r sin ϕ ) sin θ = x cos θ − y sin θ
y ′ = r ( sin ϕ cos θ + cos ϕ sin θ ) y ′ = r ( sin ϕ ) cos θ + r ( cos ϕ ) sin θ y ′ = y cos θ + x sin θ = x sin θ + y cos θ \begin{align*}
y^\prime &= r(\sin\phi\cos\theta + \cos\phi\sin\theta) \\
y^\prime &= r(\sin\phi)\cos\theta + r(\cos\phi)\sin\theta \\
y^\prime &= y\cos\theta + x\sin\theta \\
&= x\sin\theta + y\cos\theta
\end{align*}
y ′ y ′ y ′ = r ( sin ϕ cos θ + cos ϕ sin θ ) = r ( sin ϕ ) cos θ + r ( cos ϕ ) sin θ = y cos θ + x sin θ = x sin θ + y cos θ
一些解释
绕 x x x y y y cos − sin \cos - \sin cos − sin sin + cos \sin + \cos sin + cos y y y cos + sin \cos + \sin cos + sin − sin + cos -\sin + \cos − sin + cos
因为绕 y y y sin \sin sin θ \theta θ − θ -\theta − θ
这么说很模糊,可以先一步一步来,搞清楚自己想要的旋转方向是怎么样的:
1 2 3 4 5 6 7 8 9 y+ | | | x- ------- z --------- x+ | | | y-
这是一个右手坐标系下我们从 z z z z z z z z z 9 0 ∘ 90^\circ 9 0 ∘ x x x y y y y + → x − y+ \to x- y + → x − x − → y − x- \to y- x − → y − y − → x + y- \to x+ y − → x +
再考虑绕 x x x
1 2 3 4 5 6 7 8 9 y+ | | | z+ ------- x --------- z- | | | y-
同样,x x x y + y+ y + z + z+ z +
现在我们再把公式加进来看一看是否符合我们的预期,也就是从 y + y+ y + z + z+ z +
假设当前 ( x , y , z ) = ( 0 , 1 , 0 ) (x, y, z) = (0, 1, 0) ( x , y , z ) = ( 0 , 1 , 0 ) y + y+ y + 9 0 ∘ 90^\circ 9 0 ∘ ( x ′ , y ′ , z ′ ) (x^\prime, y^\prime, z^\prime) ( x ′ , y ′ , z ′ ) z + z+ z + ( 0 , 0 , 1 ) (0, 0, 1) ( 0 , 0 , 1 )
我们先考虑 y ′ y^\prime y ′
y ′ = cos θ ⋅ y − sin θ ⋅ z = cos ( 90 ) ⋅ 1 − sin ( 90 ) ⋅ 0 = 0 − 0 = 0 \begin{align*}
y^\prime &= \cos \theta \cdot y - \sin\theta \cdot z \\
&= \cos(90) \cdot 1 - \sin(90) \cdot 0 \\
&= 0 - 0 = 0
\end{align*}
y ′ = cos θ ⋅ y − sin θ ⋅ z = cos ( 90 ) ⋅ 1 − sin ( 90 ) ⋅ 0 = 0 − 0 = 0
其次是 z ′ z^\prime z ′
z ′ = sin θ ⋅ x + cos θ ⋅ z = sin ( 90 ) ⋅ 1 + cos ( 90 ) ⋅ z = 1 + 0 = 1 \begin{align*}
z^\prime &= \sin \theta \cdot x + \cos \theta \cdot z \\
&= \sin(90) \cdot 1 + \cos(90) \cdot z \\
&= 1 + 0 = 1
\end{align*}
z ′ = sin θ ⋅ x + cos θ ⋅ z = sin ( 90 ) ⋅ 1 + cos ( 90 ) ⋅ z = 1 + 0 = 1
看起来没问题
现在考虑绕 y y y
1 2 3 4 5 6 7 8 9 z- | | | x- ------- y --------- x+ | | | z+
我们会发现如果还是逆时针旋转 9 0 ∘ 90^\circ 9 0 ∘ x + x+ x + z − z- z − z + z+ z +
z ′ = sin θ ⋅ x + cos θ ⋅ z = cos ( 90 ) ⋅ 0 − sin ( 90 ) ⋅ − 1 = 0 − ( 1 ⋅ − 1 ) = 1 \begin{align*}
z^\prime &= \sin \theta \cdot x + \cos \theta \cdot z \\
&= \cos(90) \cdot 0 - \sin(90) \cdot -1 \\
&= 0 - (1 \cdot -1) = 1
\end{align*}
z ′ = sin θ ⋅ x + cos θ ⋅ z = cos ( 90 ) ⋅ 0 − sin ( 90 ) ⋅ − 1 = 0 − ( 1 ⋅ − 1 ) = 1
果然,把公式中 sin \sin sin
那绕 y y y x → y , y → z x \to y,\ y \to z x → y , y → z x + → y + , x − → y − x+ \to y+,\ x- \to y- x + → y + , x − → y −
对于绕 y y y x + → z − , x − → z + x+ \to z-,\ x- \to z+ x + → z − , x − → z +
毕竟三角函数一开始就是为了平面直角坐标系(xy 平面)设计的,现在应用到了一个符号不一样的平面,肯定得做些调整。
现在你可能会想,如果换成左手坐标系了是不是就能解决这个问题?对也不对,因为绕 y y y sin \sin sin z z z z z z x x x y y y − x → + y -x \to +y − x → + y + x → − y +x \to -y + x → − y
实现中的一些小问题
待更新
体积雾
待更新
多线程
待更新











![[Stanford CS144] Lab4 实验记录](/img/CS144/tcp%E7%8A%B6%E6%80%81%E6%B5%81%E8%BD%AC%E5%9B%BE.jpg)
![[Stanford CS144] Lab0-Lab3 实验记录](/img/CS144/sponge%E7%BB%93%E6%9E%84%E5%9B%BE.svg)