[Stanford CS144] Lab0-Lab3 实验记录

注：因为实验指导书和课程文件^[1]里都明确的写了不能公开代码，所以博客上的实验记录就主要记录思路以及一些核心代码片段，不会公开完整的仓库。

Lab0 networking warmup

Lab 要求实现一个在内存层面上可靠的字节流（ByteStream），感觉和 unix 中的管道挺像的。其实这样先进先出的结构完全可以直接使用 STL 的 queue<char> 实现，会非常简单。但是考虑到 lab 的要求是一个固定大小（capacity）的字节流，个人认为直接开个数组模拟更合适，速度也应该会更快。

具体来说，就是开一个 string（没有直接使用字符数组是因为实验指导书提到了最好使用现代 C++ 的风格，避免使用 new 来手动分配内存）来储存数据，以及一个头指针和尾指针指向字节流的开始和结尾。这样就实现了一个环形队列，peek_output() 函数的实现大概是下面这样的：

string ByteStream::peek_output(const size_t len) const {
    size_t peek_size = min(buffer_size(), len);
    size_t i = 0;
    string ret = "";
    ret.resize(peek_size);
    while (i < peek_size) {
        ret[i] = _data[(_head + i) % _capa];
        i++;
    }
    return ret;
}

不过这样的实现虽然看起来比较直观，其性能是比较差的。这主要是因为环形队列中大量的使用了取模运算，造成速度大幅下降。因为我现在还没开始做 Lab4，所以暂时没有太过考虑性能问题，Lab0 的测试结果如下（release 模式）：

[100%] Testing Lab 0...
Test project /mnt/e/ocourses/st_cs144/sponge/build
    Start 26: t_byte_stream_construction
1/9 Test #26: t_byte_stream_construction .......   Passed    0.01 sec
    Start 27: t_byte_stream_one_write
2/9 Test #27: t_byte_stream_one_write ..........   Passed    0.01 sec
    Start 28: t_byte_stream_two_writes
3/9 Test #28: t_byte_stream_two_writes .........   Passed    0.01 sec
    Start 29: t_byte_stream_capacity
4/9 Test #29: t_byte_stream_capacity ...........   Passed    0.22 sec
    Start 30: t_byte_stream_many_writes
5/9 Test #30: t_byte_stream_many_writes ........   Passed    0.01 sec
    Start 31: t_webget
6/9 Test #31: t_webget .........................   Passed    0.81 sec
    Start 53: t_address_dt
7/9 Test #53: t_address_dt .....................   Passed    0.05 sec
    Start 54: t_parser_dt
8/9 Test #54: t_parser_dt ......................   Passed    0.01 sec
    Start 55: t_socket_dt
9/9 Test #55: t_socket_dt ......................   Passed    0.01 sec

100% tests passed, 0 tests failed out of 9

Total Test time (real) =   1.17 sec
[100%] Built target check_lab0

Lab1 stitching substring into a byte bytestream

这个 Lab 需要实现一个“重排器（reassembler）”，即把不同的数据片段根据提供的起始下标重新排列成连续的字节流。并且我们还需要保证尽可能快的把收到的数据放入字节流中（即如果 $[0, i]$ 范围内的字符全部被收到了，就应该把这一段的数据立刻放入字节流中）。

先不提实验本身，实验指导书中的要求就挺难理解的，特别是 capacity 的概念。简单来说就是字节流中未读取数据的大小加上重排器的接收范围。

或者说，重排器的容量是有限的，如果某个数据段的 index 太大了，重排器可以直接抛弃。而字节流中的未读取数据越多，最小的，会被抛弃的 index 就会越小。

实现

粗略描述

实现这个重排器有很多种方法，最简单的当然是把每个到达数据片段都复制一遍，然后一发现重排器的前面有连续的数据片段就放入字节流中。

但是很明显，这样的算法是非常低效的，对于每个新到达的数据段，都必须要完整的遍历一遍，即使是之前已经接收过完全一样的数据了。

这里我采用的避免重复复制的方法是实现一个专门维护“段的集合”的数据结构。

对于任何一个新到达的数据段，我们都可以把他的范围表示成 $[l, r)$ 这样的形式。那么我们也可以维护一个段的集合，表示当前还没接收到的数据范围，用 $u$ 表示 。对于新到达的段 $x = [l, r)$，如果我们能求出 $u$ 和 $l$ 相重合的部分，或者说 $u \cap x$，我们就只需要遍历这部分了（即 $x$ 能覆盖的，还未填充的段），而如果我们发现 $u \cap x$ 的长度为 $0$ （新到达的数据不包含任何未接收部分），就可以直接返回了，避免了前面提到的重复遍历问题。

在新数据段的 $u \cap x$ 部分被写入后，我们也需要能够改变 $u$，让其去掉 $u \cap x$ 这部分，表示该段已经接收到。

例子

看这样的描述不太清晰，下面是一个例子：

假设我们的目标是接收一个 $[0, 10)$ 的数据段，那么在最开始的时候，还没有任何数据，$u$ 就是 $[0, 10)$ 这个范围。

现在接收到了一段新的数据，为 $x = [2, 5)$，那可以求出 $u \cap x = [2, 5)$，也就是 $x$ 范围内的数据完全没有重复。

在填充完 $x$ 后，我们进行 $u = u - (x \cap u)$ 的操作（注意这里的 $-$ 不表示差集，表示从 $u$ 中移除一部分），代表 $x \cap u$ 不再是未填充段。现在 $u$ 就变成了 $\{[0, 2), \ [5, 10)\}$。

现在再接收一个新数据段 $y = [1, 6)$，可以发现其完全覆盖了之前的 $x = [2, 5)$，但是我们不需要重复的去遍历之前已经被填充的部分，而是根据 $y$ 和 $u$ 求交的结果 $u \cap y = \{[1, 2), \ [5, 6)\}$ 来填充。

需求

到此为止，需要实现的数据结构就比较清晰了。我们应该先实现两个类，第一个表示单个的段（Seg），第二个表示很多段的集合（Segs）。

对于 Segs，需要有以下几个功能：

• 求出和一个 Seg 的交集，即前面提到的 $u \cap x$ 操作。
• 删去一个 Seg，即前面提到的 $u = u - (u \cap x)$ 操作。

我们知道一个 Segs 里面可能有很多个 Seg。如果我们要实现 Segs $a$ 和 Seg $b$ 的求交操作，就需要先找出 $a$ 的一个子集 $c$，这个子集里的每一个 Seg 都和 $b$ 有重合的部分，大概是下面这样的：

         1        2(c1)            3(cn)            4
Segs a : |---|    |-----|          |--------|       |---|
Seg  b :        |-----------------------|

图中 $a$ 的 2 号和 3 号 Seg 就和 $b$ 有重合部分，属于子集 $c$。

算法

可是一个一个的去遍历 $a$ 中的小 Seg 是线性的复杂度，也没比朴素算法好多少。

这里我采用的优化方法是二分。

我们设子集 $c$ 的第一个段为 $c_1$ （在上图中就是 2 号段），再设子集 $c$ 的结束段为 $c_n$（上图中的 3 号段）。

那么通过观察可以发现，$c_1$ 一定是第一个右端点比 $b$ 的左端点大的段。而 $c_n$ 一定是最后一个左端点比 $b$ 的右端点小的段。很明显，这样如同“最大化最小值”的表达是可以通过二分解决的，但前提是 Segs 类里对于多个 Seg 的储存必须是有序的。

因为 Segs 类中会处理频繁的插入和删除，我实现的时候采用了 std::set<Seg> 来储存不同的段，同时把这些段维持在一个有序的状态里，方便查询。

这样一来，查询 $c_1$ 和 $c_n$ 的复杂度就降到了 $\log(段数)$。

这个查询 $c_1$ 和 $c_n$ 的函数可以说是整个数据结构里最核心的函数了，如下，别的部分因为不公开代码的规定还是不太方便展示。

template <integral T, bool REC_LEN>
typename std::pair<typename Segs<T, REC_LEN>::s_iter_t, typename Segs<T, REC_LEN>::s_iter_t>
Segs<T, REC_LEN>::intersect_iter(const Seg<T> &b) const {
    // return the first and last iterator of the intersected segments
    // 返回第一个和最后一个和 b 有重叠的段的迭代器
    if (b.len() == 0)
        return {_segs.end(), _segs.end()};
    auto fir = fir_GT_iter_r(b.l); // 前文讲的 c1，是第一个右端点比查询段大的段
    if (fir != _segs.end() && ((*fir) ^ b).len() == 0)  // if no intersection
        fir = _segs.end();
    auto las = lst_LT_iter(b.r); // 前文的 cn，是最后一个左端点比查询段的右端点小的段
    if (las != _segs.end() && ((*las) ^ b).len() == 0)
        las = _segs.end();

    // 处理 c1 和 cn 没找到的一些情况
    if (fir == _segs.end() && las != _segs.end())
        fir = las;
    if (fir != _segs.end() && las == _segs.end())
        las = fir;
    return {fir, las};
}

然后在 StreamReassembler::push_substring，就可以直接根据 Segs 提供的范围填充数据了：

……
    // insert new arrival into _tmp
    const Seg coverage{index, index + data.size()}; // 新到达数据段的范围
    auto &&unfilled_intersect = _unfilled_segs ^ coverage; // 这里我重载了 ^ 这个符号，表示求交
    for (auto &s : unfilled_intersect) {
        // s 表示一个未填充的段
        for (size_t i = s.l; i < s.r && (i - _fir_unpushed_idx) <= _capacity; i++) {
            _tmp[i - _fir_unpushed_idx] = data[i - index];
            // 这里 _tmp[0] 对应的是 _fir_unpusehd_idx，即第一个没被放入字节流的位置
            // 所以要加一个偏移量，同时 (i - _fir_unpushed_idx) <= _capacity 确保了 _tmp 不会越界
            _unassembled_bt++;
        }
    }
    _unfilled_segs -= coverage;
    // find the first unfilled segment, before this segment, all data are filled
……

这样实现的 push_substring，性能还是比较令人满意的，如下：

[100%] Testing the stream reassembler...
Test project /mnt/e/ocourses/st_cs144/sponge/build
      Start 18: t_strm_reassem_single
 1/16 Test #18: t_strm_reassem_single ............   Passed    0.01 sec
      Start 19: t_strm_reassem_seq
 2/16 Test #19: t_strm_reassem_seq ...............   Passed    0.01 sec
      Start 20: t_strm_reassem_dup
 3/16 Test #20: t_strm_reassem_dup ...............   Passed    0.01 sec
      Start 21: t_strm_reassem_holes
 4/16 Test #21: t_strm_reassem_holes .............   Passed    0.01 sec
      Start 22: t_strm_reassem_many
 5/16 Test #22: t_strm_reassem_many ..............   Passed    0.10 sec
      Start 23: t_strm_reassem_overlapping
 6/16 Test #23: t_strm_reassem_overlapping .......   Passed    0.01 sec
      Start 24: t_strm_reassem_win
 7/16 Test #24: t_strm_reassem_win ...............   Passed    0.10 sec
      Start 25: t_strm_reassem_cap
 8/16 Test #25: t_strm_reassem_cap ...............   Passed    0.07 sec
      Start 26: t_byte_stream_construction
 9/16 Test #26: t_byte_stream_construction .......   Passed    0.01 sec
      Start 27: t_byte_stream_one_write
10/16 Test #27: t_byte_stream_one_write ..........   Passed    0.01 sec
      Start 28: t_byte_stream_two_writes
11/16 Test #28: t_byte_stream_two_writes .........   Passed    0.01 sec
      Start 29: t_byte_stream_capacity
12/16 Test #29: t_byte_stream_capacity ...........   Passed    0.20 sec
      Start 30: t_byte_stream_many_writes
13/16 Test #30: t_byte_stream_many_writes ........   Passed    0.01 sec
      Start 53: t_address_dt
14/16 Test #53: t_address_dt .....................   Passed    0.05 sec
      Start 54: t_parser_dt
15/16 Test #54: t_parser_dt ......................   Passed    0.01 sec
      Start 55: t_socket_dt
16/16 Test #55: t_socket_dt ......................   Passed    0.01 sec

100% tests passed, 0 tests failed out of 16

Total Test time (real) =   0.70 sec
[100%] Built target check_lab1

后面我还用 perf 生成过火焰图尝试继续优化一下这个实现，生成的结果如下（这个 svg 图是可以交互的，不过需要在单独的一个窗口打开）：

这里第一张是 debug 模式下的，第二张是 release 模式下的，可以看到，在 release 模式下，很多函数都被内联了，没法很好的分析。但是 debug 模式中，可以发现在 push_substring 这个函数里，Segs 的操作只使用了很少的时间，反倒是 deque 的字符串操作非常耗时，比如：

_ZNSt5dequeIcSaIcEEixEm -> std::deque<char, std::allocator<char> >::operator[](unsigned long)
_ZNSt5dequeIcSaIcEE5frontEv -> std::deque<char, std::allocator<char> >::front()

这样的函数。

很显然，用 deque 去存临时数据不是一个很好的选择，不过鉴于 Segs 的性能是比较良好的，我现在就先不改了，等到 Lab4 优化性能的时候在专门去改善一下字符串拷贝的问题。

Lab2 the TCP receiver

这个 Lab 有两个部分，第一个需要实现相对和绝对 seqno 的互相转换，第二部分才真正的使用之前实现的包装类来写 TCP receiver。

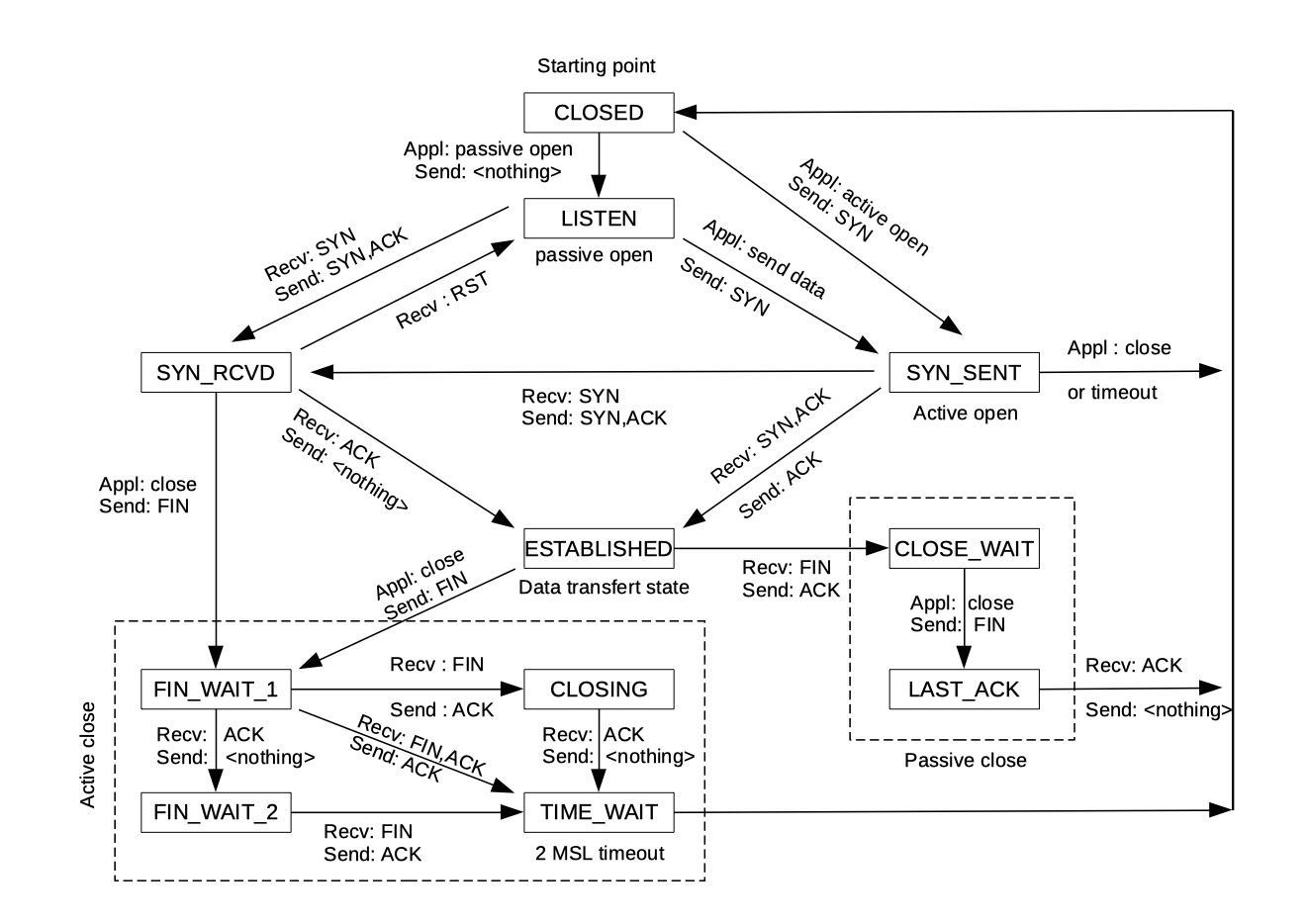
要写出这个 Lab 还得对 TCP 报头（header）有一些基本的了解。首先，一段消息在 TCP 协议中可能会被拆成很多小段传输，而每段都会有一个报头。其中的 SYN 和 FIN 分别标志着传输的开始和结束。

即，如果报头中的 SYN 标志位为真，表明这个 TCP 包是整段消息的第一个包，对于 FIN 也是同理（最后一个包）。

一般来说，我们把 0 作为一串数据中第一个的下标（比如字符数组），但是在 tcp 中不是这样的，这个第一个数据的下标是随机出来的。每个 TCP 报头都会包含一个 seqno，表示这个包中数据的启示下标，那我们知道含有 SYN 的包是整段数据的第一个包，这个包的 seqno 自就是整段数据的第一个下标，我们把这个第一个下标称为 ISN (initial sequence number)。

所以为什么要使用随机的 seqno 呢？这主要是因为防止和历史数据混淆，如果在前面的连接中，有些包发送的特别慢（在网络阻塞时），等到连接关闭了接收端才收到。这个时候，如果 seqno 不是随机出来的，刚刚历史数据的 seqno 有很大可能就在接收端的接收窗口中，被错误的接收了^[2]。

seqno 包装类

虽然这个 TCP 数据包的下标是随机出来的，但是我们使用的时候（比如之前实现的 push_substring 函数），还需要转换成从 0 开始的下标，并且这个下标和 seqno 不一样，是 64 位的。

对于这个从 0 开始的下标，实验指导书称之为 abs seqno（即绝对 seqno），我们需要写一个类来专门转换这两种 seqno。

从 abs seqno 转换到 seqno 非常简单，只需要直接返回 ISN + abs_seqno 就行了，自然溢出后直接就能得到 seqno。

但是从 seqno 转换到 abs seqno 就没那么简单了。seqno 是 32 位的，而 abs seqno 是 64 位的。同一个 seqno 可以对应多个 abs seqno。所以要实现的 unwrap 函数里面多了一个 checkpoint，转换出来的 abs seqno 需要是最接近 checkpoint 的那个。

其实这个问题还是用数学的语言来解释更加清晰一点。设 checkpoint 为 $c$，seqno 为 $s$，$M = 2^{32}$。

那么问题就转化为了：求一个 $s_a$ (asb seqno)，使得 $s_a \equiv s - \text{isn} \pmod M$，同时，最小化 $|s_a - c|$ 。

我的实现是下面这样的，第一眼看上去可能有些迷惑（实际上下面解释也挺迷惑的，我试了好几种表达方法，但碍于本人的数学和语文水平，都没法把这个想法清晰的表达出来）：

//! \param n The relative sequence number
//! \param isn The initial sequence number
//! \param checkpoint A recent absolute 64-bit sequence number
uint64_t unwrap(WrappingInt32 n, WrappingInt32 isn, uint64_t checkpoint) {
    WrappingInt32 wrapped_ckp = wrap(checkpoint, isn); 
    // 模 2^32，同时 + isn
    // 实际上是把一个绝对的 ckp 变成一个在 isn 意义下的相对 ckp 
    int32_t offset = n - wrapped_ckp;
    static constexpr uint32_t MX32 = numeric_limits<uint32_t>::max();
    int64_t ret = offset + checkpoint;
    if (ret < 0)
        return ret + MX32 + 1; 
    return ret;
} 

这里的 offset 代表的是 checkpoint + isn 到要转换的 seqno（在模 $2^{32}$ 的意义下）的距离，可以是正的也可以是负的。

0     2^32     2*2^32     3*2^32
|        |        |        |
|--------|--------|--------|
 |     |                 |
seqno  ckp + isn       ckp + isn（实际）
 |<--->|
  offset

为了得到一个和 ckp + isn 最近的 seqno，可以把刚刚得到的 offset 加到 ckp + isn 上。相当于是给 seqno 加上了某个 $2^{32}$ 的倍数。

把这个 offset + ckp + isn 减去 isn 就得到了 abs seqno （因为 seqno 和 abs seqno 就差了个 isn）。

所以 abs seqno 就等于 offset + ckp。

不过，直接这样计算可能会有得不到最优解，下面就是直接采用这个方法的计算结果：

0     2^32     2*2^32     3*2^32
|        |        |        |
|--------|--------|--------|
                   |     |               
                  seqno  ckp + isn      
                   |<--->|
                    offset

可以看到，如果直接给当前 seqno 加上 $2^{32}$，其与 ckp + isn 的距离会更近。同时也符合前面提到的 $s_a \equiv s - \text{isn} \pmod M$。

可以思考一下，这样得不到最优解的情况只会发生在 $|\text{offset}| > 2^{32} \div 2$ 的情况下。

因为我们给 seqno 加上任意的 $2^{32}$ 的倍数，其在模 $2^{32}$ 的意义下是不变的。但是在 seqno 加这个倍数的同时，offset 是会变化的（而我们希望最小化 offset）。

比如 $\text{offset} = -2^{32} + 1$ （这肯定符合 $|\text{offset}| > 2^{32} \div 2$）。那么

$$\begin{align*} &(\text{offsset} + 2 ^ {32}) = 1 \end{align*}$$

像刚才那样的例子，直接给 seqno 加上 $2^{32}$ 就变成了：

2^32     2*2^32   3*2^32   4*2^32
|        |        |        |
|--------|--------|--------|
                |  |                 
        ckp + isn  seqno       
                <-->
                offset   

这时候，利用自然溢出，我们自己根本不用处理这个问题。

注意到在代码里面，储存 offset 的类型是 int32_t，其有符号，储存的范围刚好是 $[-2^{32} \div 2, 2^{32} \div 2 - 1]$。

所以一旦 $|\text{offset}| > 2^{32} \div 2$，offset 就会“自动”给自己加上或减去 $2^{32}$ 的倍数，来最小化自己。

当然，这样的实现还是有 bug 的，比如下面这样：

0                      2^32
|-----------------------|
  |                  |
  ckp+isn            seqno
  |<---------------->|
          offset  

很明显，这里的 offset 是正数，并且大于 $2^{31}$。虽然这个时候给 seqno 减去一个 $2^{32}$ 会让 offset 的绝对值更小，但是这会让 seqno 变成负数，显然是不行的。所以写了下面这几行来防止出现负数，即，如果出现了负数就把这个 $2^{32}$ 加回去。

static constexpr uint32_t MX32 = numeric_limits<uint32_t>::max();
    int64_t ret = offset + checkpoint;
    if (ret < 0)
        return ret + MX32 + 1; 

。

---

1. 1.https://cs144.github.io/logistics.pdf ↩
2. 2.https://www.zhihu.com/question/53658729 ↩