USACO23JAN Find and Replace S（洛谷 P9013）题解

题目链接

博客中观看体验更佳

分析

题意非常简洁，即问你通过一系列的字符替换，最少花多少步能把一个 $s$ 串变成 $t$ 串。

拿到题之后，可以先从样例开始分析。

从 $\texttt{BBC} \to \texttt{ABC}$ 这个样例可以发现，不可能同时把某个字符替换成两个字符（$\texttt{BB} \to \texttt{AB}$），会起冲突。

那直接统计 $s_i \ne t_i$ 的个数（给串去重之后，即不存在 $s = \texttt{AA}, t = \texttt{BB}$ 这种）就可以作为答案了吗？可以从最后一个样例发现不是这样的。

环的处理

因为最后一个样例中，$\texttt{CD}$ 的部分是一样的。我们直接考虑 $\texttt{AB} \to \texttt{BA}$ 的变换。如果直接执行 $\texttt{A} \to \texttt{B}$ 的操作，会得到一个 $\texttt{BB}$ 的串。这个时候就有了和前面一样的问题，不能将其转换成 $\texttt{BA}$。执行 $\texttt{B} \to \texttt{A}$ 也是同理。

解决的办法就是先执行 $\texttt{AB} \to x\texttt{B}$ 再处理 $x\texttt{B} \to \texttt{BA}$。（$x$ 是任意别的字符）

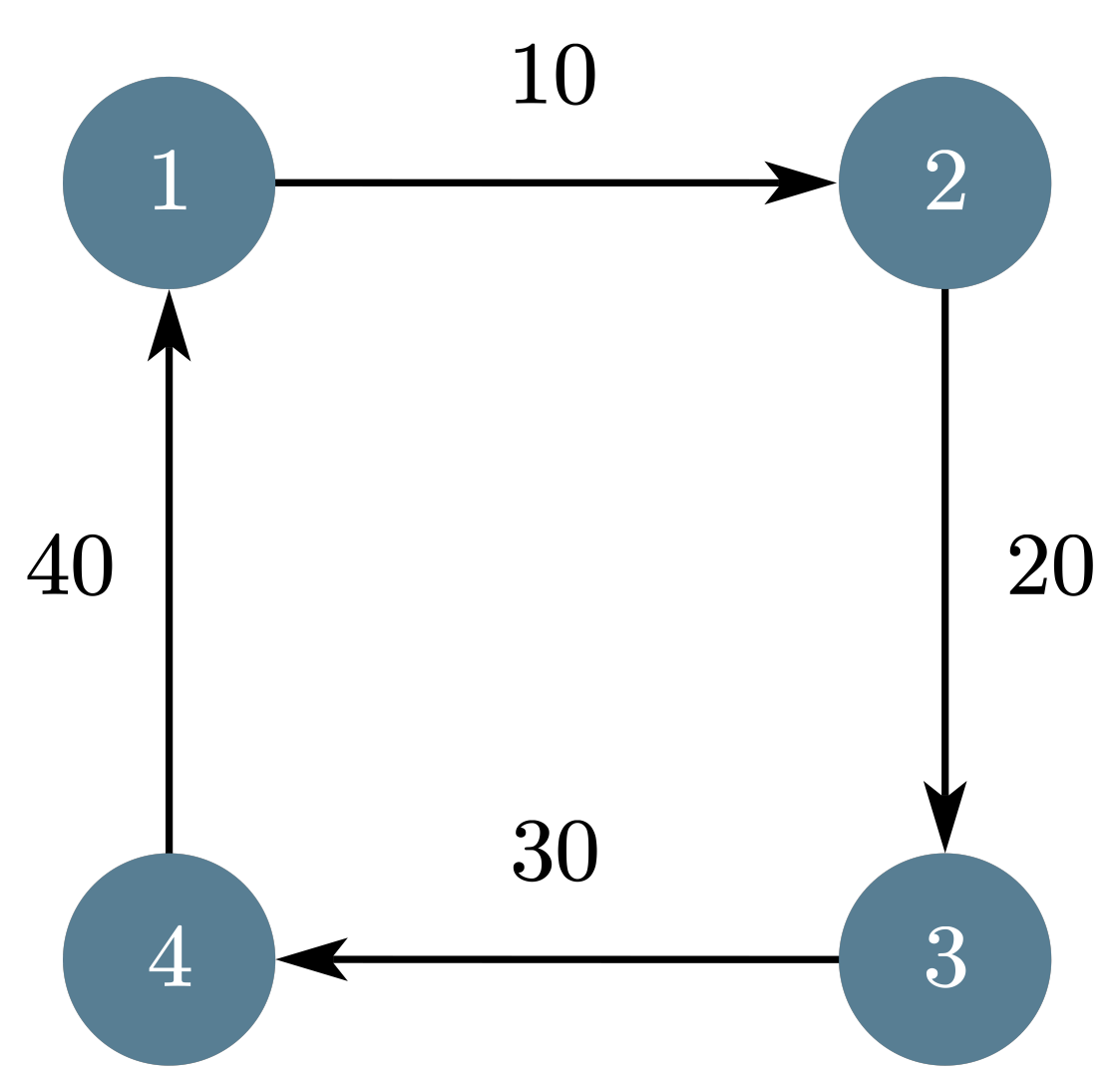
是否所有“相互依赖”的情况下，都可以通过这种方式解决呢？我们可以再思考一个大一点的样例 $\texttt{ABCD} \to \texttt{BCDA}$，用图（创建 $s_i \to t_i$ 的边，并且去掉重边和自环）的方式表示出来会更加清晰：

可以发现，这是一个环。无论我们先执行哪种 $x \to y$ 的变换，都会需要再执行 $y \to z$ 的变换。因为 $y$ 希望能变成别的。这个时候，先前 $x$ 会跟着一起被变成 $z$。

不过，如果能“化环为链”，就可以解决问题了。比如我们可以先执行 $\texttt{A} \to x$，这个链就会变成：

这样，就有一个执行 $x \to y$ 后，不用再执行 $y \to z$ 的地方了。即 $\texttt{D} \to \texttt{A}$ （执行完之后， $\texttt{C} \to \texttt{D}$ 也符合这个条件，我们倒着的按照链的顺序就可以把整条串转换为目标）。

从这两个例子可以看出，在一般的情况下，一个操作能把环转化为链，或者把链的长度（边的数量）减少 1。

所以答案的数量就是（环的数量 + 链的长度）了吗？

两种特例

1

首先，化环为链的操作需要一个不在环中出现的字符，假设环包含了字符集中所有的字符，我们是不能处理的。

假设我们的字符集只有 $\texttt{A} \sim \texttt{D}$ 这四个字符，那处理下面这个例子时候，就会发现问题。

不管先把 $\texttt{A}$ 变成什么字符，这个字符之后都会再经历最少一次的变换，导致 $\texttt{A}$ 不能被转换成目标字符 $\texttt{B}$。

当然，我们处理不了的情况不一定要求整张图中只有一个环，只要符合：

1. 所有节点都在环里
2. 字符集中的所有字符都被用到了

就不能处理了，比如下面这个例子，有两个环还是不行（字符集为 $\texttt{A} \sim \texttt{C}$）：

2

考虑这样一个输入：$\texttt{ABCDEF} \to \texttt{BCDABE}$

我们可以在一个操作内即化环为链，又把链的长度减少 1。观察到 $\texttt{A}$ 和 $\texttt{E}$ 都希望能被转换成 $\texttt{B}$。从字符转换的角度来说，$\texttt{A} \to \texttt{B} \And \texttt{E} \to \texttt{B}$ 和 $\texttt{A} \to \texttt{E} \And \texttt{E} \to \texttt{B}$ 的最终结果和操作步数都是一样的。但是第二种方法在执行 $\texttt{A} \to \texttt{E}$ 时，也把环中的一个字符转换成了环外的字符，将环化成了链。

能这么做的前提条件是，有多个环外字符希望变成环内的一个字符。更严谨的说就是环中某个节点的入度大于等于 2。

到此为止，所有的情况都基本分析好了，可以写出以下的总结（括号中的为实际判断方法）：

1. 一个字符希望转换成多个字符是无解的。（节点出度最多为 1）
2. 所有节点（所有可能的字符）全部在环中是无解的 （每种字符的入度都为 1）。
3. 答案 = 边的数量 + 绝对环的数量（环中每个节点的入度出度都为 1）

这里第二点的判断方法可以稍微解释一下：

没有选择使用出度是考虑到了环连着树的情况，参考上图。

代码实现

实现的时候找环的部分需要注意一下，其他部分都比较简单。

我们知道 tarjan 算法就可以判环，不过这道题可以用“简化版”的 tarjan，不用记录访的时间戳。我们把 dfs 的时候把所有访问过的节点从队尾压入一个双向队列。

如果我们开始 dfs 的时候是从一个环上的点进入的，之后一定会访问到一个和队头一样的节点。这个时候把所有在队头和队尾之间的节点都弹出，就得到了环中的所有节点。

如果我们发现某个节点之前访问过，但是并不在队头，就可以确定队列中的节点都不是“绝对环”，因为有树连着他（参考上图，如果从 F 节点开始搜就会出现这种情况）。

#include <bits/stdc++.h>
using namespace std;

const int CHSZ = 52;  // char set size
int out[CHSZ + 1];   // 出度只能有一个
int lpid[CHSZ + 1];  // 环的 id，不知道 -> -1，不是环 -> 0，是环 -> 1,2,3...
enum LP_STAT { UNKNOWN = -1, NOT_ABS_LP = 0 };
deque<int> vised_dq;   // 用于在找环的时候储存信息
bool vised[CHSZ + 1];  // 用于在找环的时候储存信息

set<int> in_nds[CHSZ + 1]; // in nodes，入度可以有多个
int in1_cnt = 0; // 入读为 1 的节点的数量

int abs_lp_cnt = 0;  // 绝对环数，即环不连树的环数
int diff_chs = 0;

void init() {
    memset(out, 0, sizeof(out));
    fill(lpid, lpid + CHSZ + 1, UNKNOWN);
    vised_dq.clear();
    memset(vised, 0, sizeof(vised));
    for (int i = 0; i <= CHSZ; i++) in_nds[i].clear();
    in1_cnt = 0;
    abs_lp_cnt = 0;
    diff_chs = 0;
}

inline int ch2id(char x) {
    // char to id
    if (x >= 'a' && x <= 'z') return x - 'a' + 1;
    if (x >= 'A' && x <= 'Z') return x - 'A' + 27;
    return -1;
}

bool check_loop_connect_to_tree() {
    for (int cur : vised_dq) 
        if (in_nds[cur].size() >= 2) 
            // 有树连这个环
            return true;
    return false;
}

void fill_lpid_in_vised_dq(int val) {
    for (int cur : vised_dq)
        lpid[cur] = val;
    vised_dq.clear();
}

void mark_loop(int cur) {
    if (vised[cur] && vised_dq.front() != cur) {
        // 从一个树进入的环，不是绝对环
        fill_lpid_in_vised_dq(NOT_ABS_LP);
        return;
    }
    vised[cur] = true;
    if (out[cur] == cur) {
        // 没有出度，找到一个链
        fill_lpid_in_vised_dq(NOT_ABS_LP);
        return;
    }

    if (vised_dq.size() && vised_dq.front() == cur) {
        // 找到环
        if (!check_loop_connect_to_tree()) {
            // 如果环不连树
            abs_lp_cnt++;
            fill_lpid_in_vised_dq(abs_lp_cnt);
        } else {
            fill_lpid_in_vised_dq(NOT_ABS_LP);
        }
        return;
    }
    vised_dq.push_back(cur);
    mark_loop(out[cur]);
}

void solve(const string& origs, const string& tars) {
    // orig str -> tar str
    init();
    for (int i = 0; i < origs.size(); i++) {
        int och = ch2id(origs[i]);
        int tch = ch2id(tars[i]);
        if (out[och] && out[och] != tch) {
            // 如果 o 串已经有要转换的字符，但是不是 t
            // 串的字符，那么会产生多对一
            cout << -1 << '\n';
            return;
        }
        if (!out[och]) {
            out[och] = tch;
            in_nds[tch].insert(och);
            if (och != tch) 
                diff_chs++;
        }
    }
    for (int i = 1; i <= CHSZ; i++) {
        if (in_nds[i].size() == 1) 
            in1_cnt++; // 统计入度为 1 的节点数量
    }
    for (int i = 1; i <= CHSZ; i++) {
        if (out[i] && lpid[i] == UNKNOWN) {
            // 标记环
            vised_dq.clear();
            memset(vised, 0, sizeof(vised));
            mark_loop(i);
        }
    }
    if (origs != tars && in1_cnt == CHSZ) {
        // 判断是否全部都在环中，用入度为 1 的数量来判断
        cout << -1 << '\n';
        return;
    }
    cout << diff_chs + abs_lp_cnt << '\n';
}

int main() {
    int t;
    cin >> t;
    while (t--) {
        string origs, tars;
        cin >> origs >> tars;
        solve(origs, tars);
    }
}