CF1665C题解
题目链接
博客中观看体验更佳
1.题意:
给你一个有 nnn 个节点的树,一开始,每个节点都是健康的。每秒钟你可以进行下面两种操作:
传播:对于一个节点,如果它的至少一个子节点被感染了,那么可以感染它的另一个子节点。(如果有多个节点符合条件,那一秒钟就可以传播多个节点)
注射:你可以任选树中的一个节点进行感染。(一秒钟只能多感染一个节点)
现在问你最少需要多少秒才能感染整个树。
2.思路:
看完题我们要注意到,这个题说的是节点可以把病毒传播给他们的兄弟节点,而不是传播给他们的子节点,所以这个树的每一层之间是完全独立的,不可能把病毒从一层传播给另一层。
所以我们肯定需要在一开始的时候就给每个节点的至少一个子节点注射病毒(具体哪个不重要),这样每秒钟能感染的节点更多(根据操作 1)。
那先给谁的子节点注射呢?考虑先被注射的子节点会有更多的时间把病毒传播给更多的子节点。所以我们应该先给子节点更多的节点注射病毒。
(如果先给子节点少的节点注射,那在给所有节点注射完之前,这个节点的所有子节点可能都被感染了,也就是有很多时间被浪费了)。
在确保每个节点都有至少一个子节点被注射后,我们还可以给子 ...
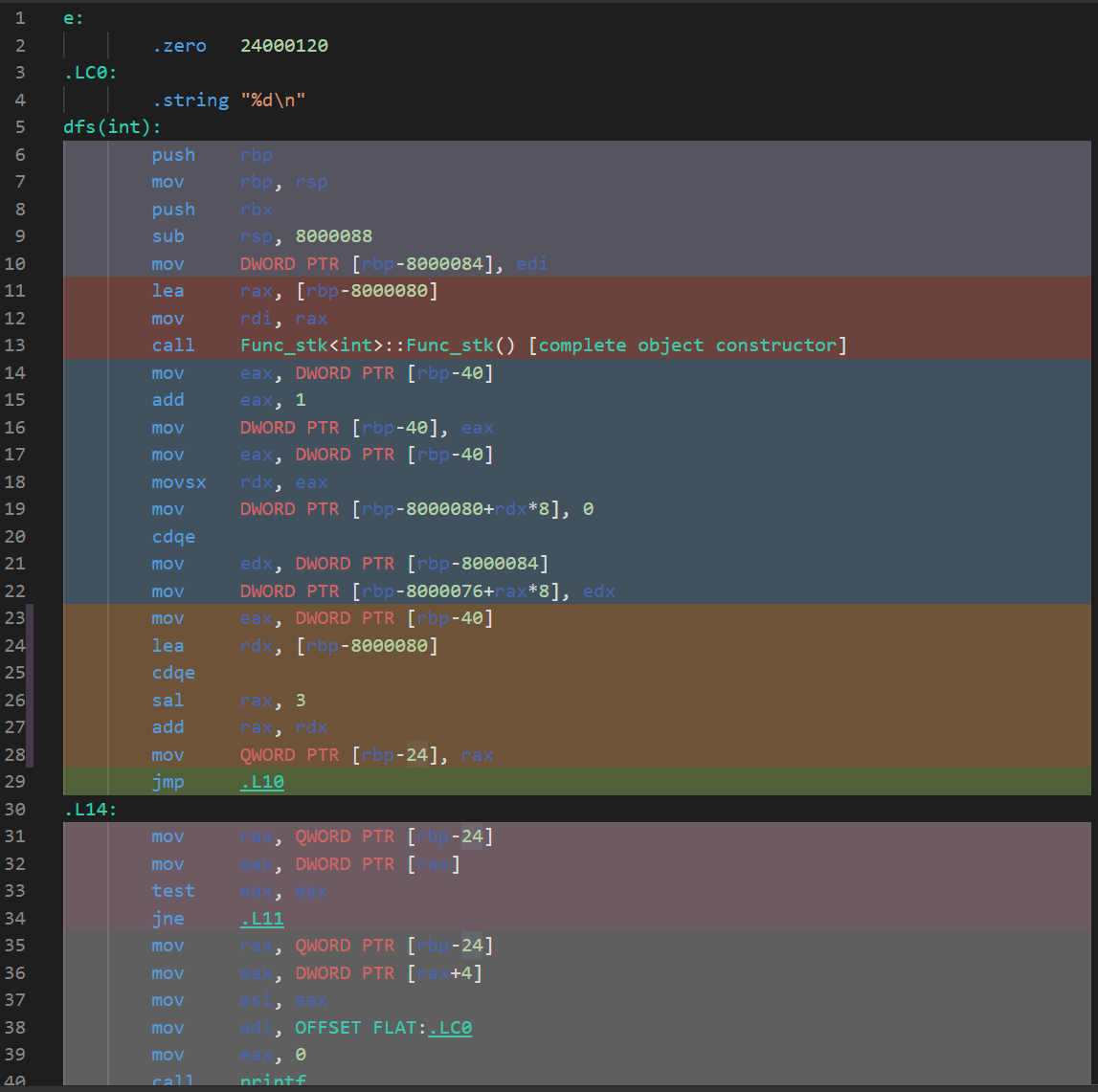
浅谈函数调用的实现
upd@2022/12/18:感谢@adpitacor和@iterator_traits在评论区中指出的几个错别字,现在已经修正
upd@2022/11/24:这篇文章能入选洛谷日报我也是很惊喜。同时深感以前写的东西水平不太行,不过既然入选了日报,还是希望尽量能把文章的水平提高一点的。显然我不可能把整个文章重写一遍,但是可以加入一些自己这段时间新学到的东西,比如栈溢出攻击和 backtrace 的实现,所以赶在发表之前把他们添加了进来。
除了内容上的变化,这次更新还修复了一些错别字,这主要需要感谢 @cancan123456 在洛谷评论区的提醒。文章发出后有很多洛谷的朋友在评论区提醒和提出建议。比如 @szTom指出了 __fastcall 的影子空间。@LiuTianyou 介绍了强制内联的方法(这次新加的内容就使用了强制内联,以前属实是太菜了不知道有这个东西),以及调用约定中的 thiscall。@小菜鸟 提到了 longjump 函数(和本文中的一次返回多个函数有关)。 非常感谢这些网友,在学会了这些东西后我会考虑把它们陆续加进来,如果你有别的任何建议也欢迎像他们一样在评论区提 ...
洛谷 P8270 [USACO22OPEN] Subset Equality S 题解
题目连接
博客中观看体验更佳
1:题意
给你两个字符串,sss 和 ttt ( sss 和 ttt 的长度都不超过 10510^5105 )。再给你一些询问 ( 询问数量不超过 10510^5105 ),每个询问为小写字母 'a' 到 'r' 的子集,对于每个询问,请你回答在 sss 串和 ttt 串只包含询问中给定的字母时是否相等。
2:分析
2.1:暴力
很容易想到暴力的方法,对于每个询问,我们可以只考虑包含在集合中的字符,然后对比两个字符串。当然,这样我们就会需要对于每个询问重新遍历一遍字符串,复杂度也会到达 n2n^2n2 ( nnn 为询问的数量和字符串的长度)。通过这个方法,我们可以拿到这道题的部分分。
不过如何才能拿到其他分数呢?
2.2:简化问题
直接解决这个问题可能太复杂了,我们可以试试看化简一下这个问题,再把化简过的解法推广到原问题。
我们首先考虑询问中只包含两个字母的情况。设这两个字母为 a 和 b。那么我们如何判断两个只包含 a 和 b 的字符串是否相等呢?
首先需要考虑的肯定是两个串中 a 和 b 的数量是否相等,如果 a 和 b 的数量不等,那这两个串一定不 ...
P8269 [USACO22OPEN] Visits S 题解
题目连接
博客中观看体验更佳
1:题意简述
有 NNN 个奶牛,奶牛 i(1≤N)i (1 \le N)i(1≤N) 想访问奶牛 ai(ai≠i)a_i (a_i \ne i)ai(ai=i) 。如果 aia_iai 已经离开去访问别的奶牛了,则 iii 不能成功访问 aia_iai,否则,这次成功访问可以增加 viv_ivi 次哞叫。 现在让你找出可能的最大哞叫次数
2:分析
理解题目后,我们可以首先分析下样例,试试看找一些有用的信息。
为了方便分析样例,我们可以把样例用图的形式展示,图中有向边连接的两个节点就是一头牛和这头牛希望访问的牛 ( iii 和 aia_iai )。而边权是这次访问能产生的哞叫次数。
通过这张图,我们可以发现,不管以什么样的顺序访问,最多都只能成功的访问三次,最后的一次访问一定会遇到之前已经遇到过的牛,所以选择 2→32 \rarr 32→3,3→43 \rarr 43→4 和 4→14 \rarr 14→1 可以达到最大的哞叫次数,也就是 20+30+40=9020 + 30 + 40 = 9020+30+40=90 次。
再仔细思考这个样 ...
P8187 [USACO22FEB] Robot Instructions S 题解
目录:
暴力
折半搜索 + map 或是哈希表
折半搜索 + 双指针 + 和 dfs 不同奇怪的状态枚举方式
第一种双指针
第二种双指针
完整代码
题目链接
博客中观看体验更佳
1. 题意
给你 nnn 个二维的向量,对于任意一个 k(1≤k≤n)k (1 \le k \le n)k(1≤k≤n),求出有多少选取的方案能满足在这 nnn 个向量中选 kkk 个,并且他们的和为 (xg,yg)(x_g, y_g)(xg,yg)。
2. 分析
2.1 暴力算法
看到这个题我们可以比较快的想到拿部分分的做法,就是暴力枚举所有的选取方案,然后看他们加起来是否等于目标向量,再把符合要求的方案累加到答案中。但是我们发现 n=40n = 40n=40,并且这个算法的复杂度是 2n2^n2n 的,所以一定会超时。
2.2 折半搜索 + map 或者是哈希表
2.2.1 简要思路
这道题中的折半搜索指的是把 nnn 种向量分成两部分,对这两个部分分别用暴力的方法求出所有可能的选取方案,再把这些选取的方案,以及这个方案的结果(他们的和)按照某种方案储存下来,最后匹配这两部分的方案,把符合题目 ...
P8095 [USACO22JAN] Cereal 2 S题解
前言:题解可能比较啰嗦,因为这题比赛的时候没做出来,所以写题解主要用于整理自己的思路。如果你有思路只是代码打挂了简易直接跳到代码部分。
update@2022/3/13: 感谢@小木虫的提醒,当前的解法不是正解! 如果USACO的数据够强的话,目前我使用的匈牙利算法因为复杂度是 O(nm)O(nm)O(nm),是过不了这道题的。如果想用我这个二分图匹配 + 拓扑的方法实现,可以使用dinic算法求二分图最大匹配(不过写起来会比较麻烦)。本人有时间的时候也会尝试用dinic实现这个解法并且更新题解。
题目链接
博客中观看体验更佳
1:题意
有 NNN 头牛,MMM 种麦片(每种一箱),每头都有第一和第二喜欢的麦片种类(下文简称为一选和二选),牛会优先选择自己最喜欢的麦片,当最喜欢的麦片被占用后会选择第二喜欢的麦片,问:
最少会有多少牛得不到麦片。
能达到此最小值的牛的排列
2:分析
2.1 第一小问
对于第一个小问,可以发现这是一个标准的二分图最大匹配问题,很容易想到使用匈牙利算法解决(然而这次比赛的时候我并没有想到)。不熟悉匈牙利算法和二分图匹配问题的同学可以参考模板题里的题解。这 ...
P7995 [USACO21DEC] Walking Home B 题解
1:题意
给定一个 N×NN \times NN×N 的区域,区域中的每个点由 0 或 1 组成,1 类点不能走 0 类点可以走。问你从左上角走到右下角,并且最多转向 KKK 次有多少种走法。
2:分析
看到在格子图中问有多少走法的题目,可以比较容易的想到使用 dp 算法解决,具体做法参考 P1002过河卒,但是本题的难点以及本题解的重点在于如何处理对于转向次数的限制。
根据上图,我们可以看到,路径是否包含转向不仅跟从哪个点转移来有关,还和转移来的那个点是从哪个点转移来的有关(从左边或是从右边)。具体的判断规则如下,可以对照着图来理解:
如果当前点是从上面的点 map[i - 1][j] 转移来的,并且上面那个点是从他的左边转移来的,那么会发生一次转移。(图中当前点上方的蓝色虚线)
如果当前点是从左边的点 map[i][j - 1] 转移来的,并且左边那个点是从他的上方转移来的,那么会发生一次转移。(图中当前点左方的蓝色虚线)
其他所有情况不会发生转向
我们让 dp[i][j][k][t] 表示走到 (i,j)(i,j)(i,j) ,花费了 kkk 次转向,并且是从左边 (0) ...
P2867 [USACO06NOV]Big Square S 题解
1:理解题意:
给定一个 N×NN\times NN×N 的区域,并且这个区域内有两类点,J 类与 B 类。现在让你在区域中添加一个J类点(也可以不添加,并且添加时不能添加到已经存在 B 类点的地方),然后找出最大的由 J 类点构成的正方形。
2:分析
2.1:概括
因为数据较小 (N<100)(N<100)(N<100),并且我们可以通过一条J边来确定正方形的剩下两条边,所以可以尝试通过枚举J边,并且加以判断的方法找到最大的正方形。
2.2:一点点数学
假设我们通过两点 P1P_1P1 和 P2P_2P2 确定了一条直线,并且 P1P_1P1 的纵坐标总是比 P2P_2P2 高,那么我们可以画出下图:
可是我们如何计算出 P3P_3P3 和 P4P_4P4 的坐标呢?
首先通过观察,我们可以发现图中的四个三角形都是全等的,我们只要计算出三角形的长直角边和短直角边的长度(或者说是两个不同的直角边,只是在这种特殊情况下,长边和短边的位置是图中的样式),再加上一个偏移量,就可以得到 P3P_3P3 和 P4P_4P4 的坐标了。
三角形的长直角边:
L△ ...
P3087 [USACO13NOV]Farmer John Has No Large Brown Cow S 题解
题目链接
博客中观看体验更好
前言:这篇题解写的可能比较啰嗦,主要时是因为我把所有思考的过程都写下来了,所以如果你已经有了基本的思路,或者是希望找一篇简洁的题解,就可以跳过这篇题解了。
1:理解题意
总共有 cowcowcow 头牛,typetypetype 类形容词,有 numinum_inumi 个第 iii 类形容词,第 iii 类的第 jjj 种形容词是 adji,jadj_{i,j}adji,j ,每头牛都需要有这 typetypetype 类形容词按照顺序来修饰。现在告诉你要删除这 cowcowcow 头牛中的 nnn 头,问你在这剩下的 cow−ncow-ncow−n 头牛中,按照字典序排序,排在第 kkk 位的牛是哪一头?
2:分析和转化问题
2.1:和数字系统的关联
单看这样的描述可能有些抽象,现在我们来看一下样例是怎么样的,再在样例的基础上思考应该怎么解决这道题。
在样例中 n=3n=3n=3,k=7k = 7k=7。adji,jadj_{i,j}adji,j的值如下
adji,jadj_{i,j}adji,j
j=1j=1j=1
j=2j=2j=2
...
P2944 [USACO09MAR]Earthquake Damage 2 G题解
看到题解里面还没有用STL vector做的,所以我就来交一发。
题目链接
1:转化题意
在一张图中,一共有 ppp 个节点,ccc 条双向边,有 nnn 个节点不能删除,求出最少需要删除多少个节点才能使得这 nnn 个固定点都到达不了111号节点。
2:分析和建模
在完成题意的转化之后,我们发现题目要让我们删除一些点(尽量少),使得整张图变成两个不连通的部分,网络流算法中的最小割(最大流)算法可以处理这这个问题。
【不熟悉最大流算法的同学可以先做一下模板题】
最大流模板
但是我们又发现,一般的最小割处理的是 “删除图的一部分边使得图的两部分变得不连通” 而这道题目让我们删除的是图中一部分节点。于是我们就需要把节点转换成边。
我使用的方法是把每一个节点拆分成两个节点(出点和入点),具体的做法可以参考
P1345 奶牛的电信Telecowmunication
这道题中的题解。
这里来简单解释一下这种做法:首先,我们把图中的每一个点拆分成两个点:出和入点。
并且这两个节点之间有一条单向边连接
每条指向这个点的有向边都只能连接这个点的入点。并且从这个节点出发的有向边都只能从它的出点出发。
...

![洛谷 P8270 [USACO22OPEN] Subset Equality S 题解](/img/USACO_logo.png)
![P8269 [USACO22OPEN] Visits S 题解](https://cdn.luogu.com.cn/upload/image_hosting/45pac1tr.png)
![P8095 [USACO22JAN] Cereal 2 S题解](https://cdn.luogu.com.cn/upload/image_hosting/63og5ij1.png)
![P7995 [USACO21DEC] Walking Home B 题解](https://cdn.luogu.com.cn/upload/image_hosting/wv4kqqh6.png)
![P2867 [USACO06NOV]Big Square S 题解](https://cdn.luogu.com.cn/upload/image_hosting/e02vw603.png)
![P2944 [USACO09MAR]Earthquake Damage 2 G题解](https://cdn.luogu.com.cn/upload/image_hosting/0jw7wfno.png)


![[Stanford CS144] Lab4 实验记录](/img/CS144/tcp%E7%8A%B6%E6%80%81%E6%B5%81%E8%BD%AC%E5%9B%BE.jpg)
![[Stanford CS144] Lab0-Lab3 实验记录](/img/CS144/sponge%E7%BB%93%E6%9E%84%E5%9B%BE.svg)