题目链接(CF ,洛谷) | 强烈推荐博客 中观看。
题意
给你一个 n × m n \times m n × m 1 ≤ n , m ≤ 1000 1 \le n, m \le 1000 1 ≤ n , m ≤ 1000 − 1 -1 − 1 1 1 1 ( 1 , 1 ) (1, 1) ( 1 , 1 ) ( n , m ) (n, m) ( n , m ) 0 0 0 a i , j a_{i, j} a i , j a i + 1 , j a_{i + 1, j} a i + 1 , j a i , j + 1 a_{i, j + 1} a i , j + 1
思路
看到这个 (1 ≤ n , m ≤ 1000 1 \le n, m \le 1000 1 ≤ n , m ≤ 1000 别学我 ),所以得想一些别的办法。
首先,如果经过奇数个格子,或者说 n + m − 1 n + m - 1 n + m − 1 − 1 -1 − 1 1 1 1
直接判断某个格子图是否符合要求太麻烦,我们可以思考,如果有任意一条路径,我们是否能根据这条路径的值(也就是途径的格子的和),来做一些改变,最后让路径的值变为 0 0 0
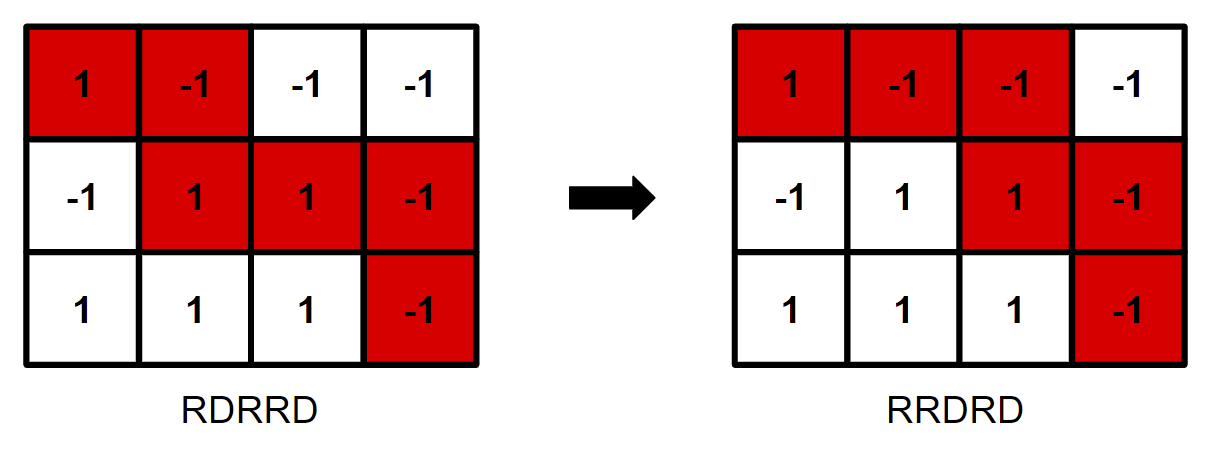
如下图这样就是对路径做了一次改变(改变前后只有一个格子不同)。最后让路径的值产生了变化。
在一次改变中,路径的值会产生 − 2 ( − 1 → 1 ) , 2 ( 1 → − 1 ) -2 (-1 \rarr 1), 2 (1 \rarr -1) − 2 ( − 1 → 1 ) , 2 ( 1 → − 1 ) 0 ( 1 → 1 OR − 1 → − 1 ) 0 (1 \rarr 1 \operatorname{OR} -1 \rarr -1) 0 ( 1 → 1 OR − 1 → − 1 ) 0 0 0
显然是不行的,如果整个格点图全是 − 1 -1 − 1 1 1 1
首先就得确保在这个格点图中不会只有值特别离谱的路径,如果只有值特别离谱的路径,那无论你怎么变,也搞不出值为 0 0 0
所以我们需要找出值最大的路径,以及值最小的路径。
设值最大的路径的值为 p max p_{\max} p m a x p min p_{\min} p m i n
那么如果:
p min ≤ 0 ≤ p max p_{\min} \le 0 \le p_{\max}
p m i n ≤ 0 ≤ p m a x
我们就一定可以通过这样的变化把任意一个值为偶数的路径变为值为 0 0 0
或者可以这样理解,如果符合上面那个条件,那我们就可以逐渐把值最小的路径向值最大的路径变换,在这个过程中,一定有一个路径的值等于 0 0 0
至于求这样的格子图的最大和最小路径,就属于是典中典了(用 dp),这里不赘述,如果有不熟悉的可以看洛谷P1004 。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <bits/stdc++.h> using namespace std;int main () int t; scanf ("%d" , &t); while (t--) { int n, m; scanf ("%d%d" , &n, &m); int a[n + 1 ][m + 1 ]; int mx[n + 1 ][m + 1 ], mn[n + 1 ][m + 1 ]; memset (a, 0 , sizeof (a)); memset (mx, 0 , sizeof (mx)); memset (mn, 0 , sizeof (mn)); for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j <= m; j++) { scanf ("%d" , &a[i][j]); } } for (int i = 1 ; i <= n; i++) mx[i][1 ] = mn[i][1 ] = mx[i - 1 ][1 ] + a[i][1 ]; for (int j = 1 ; j <= m; j++) mx[1 ][j] = mn[1 ][j] = mn[1 ][j - 1 ] + a[1 ][j]; for (int i = 2 ; i <= n; i++) { for (int j = 2 ; j <= m; j++) { mx[i][j] = max (mx[i - 1 ][j], mx[i][j - 1 ]) + a[i][j]; mn[i][j] = min (mn[i - 1 ][j], mn[i][j - 1 ]) + a[i][j]; } } if (mx[n][m] & 1 || mn[n][m] > 0 || mx[n][m] < 0 ) { printf ("NO\n" ); } else { printf ("YES\n" ); } } }




![[Stanford CS144] Lab4 实验记录](/img/CS144/tcp%E7%8A%B6%E6%80%81%E6%B5%81%E8%BD%AC%E5%9B%BE.jpg)
![[Stanford CS144] Lab0-Lab3 实验记录](/img/CS144/sponge%E7%BB%93%E6%9E%84%E5%9B%BE.svg)