B. Making Towers

思路

观察题面上给第一个样例提供的图：

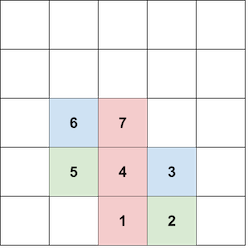
可以发现，如果我们要让某种颜色形成一个塔，除非多个相同颜色在 cc 数组中挨在一起，可以直接向上排布。就一定需要在排布该颜色后，向两侧放一些其他颜色，然后又往相反方向放置，最后使得两个颜色相同的块在一条直线上，大概是下面这样：

1
2
3
4
⬆->->->A
⬆<-<-<-A<-<-<-⬆
        A->->->⬆
        1 2 ... z

其中， AA 表示一个颜色的塔，而箭头表示放置颜色块的路径。

观察发现，在放置两个 AA 之间，需要放置偶数个其他颜色块，下面是解释：

假设第一个 AA 的位置是 (x,y)(x, y)，并且我们往右侧放置的其他颜色块的数量是（也可以是左侧） zz。

那么为了把第二个 AA 搞到 (x,y+1)(x, y + 1) 上，就需要在 (x+1,y)∼(x+z,y)(x + 1, y) \sim (x + z, y) 和 (x+1,y+1)∼(x+z,y+1)(x + 1, y + 1) \sim (x + z, y + 1) 这些位置上放置颜色块，共计 2z2z 个块，因此是偶数（直接网上堆的话是 00 个，也是偶数）。

这就意味着，假设有两个相同的颜色块 AA 和 BB，它们在 cc 数组中的位置分别是 ii 和 jj。只有 ∣i−j∣\lvert i - j \rvert 为奇数时，才可能把 AA 叠到 BB 上面，或是 BB 叠到 AA 上。

并且，只有 ii 和 jj 的奇偶性不同，∣i−j∣\lvert i - j \rvert 才可能为奇数。

然后就可以使用 dp 的方法来解决这个题目，我们对每种颜色都重复一遍相同的 dp 过程（其实更像是递推）。设 dpidp_i 为 cc 数组中，使用 ii 个该颜色的块最高能垒成多高的塔。

那么 dpidp_i 就可以从 dp0∼i−1dp_{0 \sim i - 1} 中转移而来（ +1+1 ），并且如前面所说 dpidp_i 和 dp0∼i−1dp_{0 \sim i - 1} 的奇偶性应该不同。

同时，我们需要找的是，最近的奇偶性不同的块，要不然可能造成浪费，或者是在前面已经放过的位置又放了一个块。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//author: tzyt
#include <bits/stdc++.h>
using namespace std;
#define ll long long
int main() {
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        int c[n + 1];
        vector<int> cpos[n + 1], ans(n + 1);
        set<int> unqc; // 储存所有不同的颜色
        for (int i = 1; i <= n; i++) {
            cin >> c[i];
            cpos[c[i]].push_back(i);
            unqc.insert(c[i]);
        }
        int dp[n + 1];
        for (int cur : unqc) {
            fill(dp, dp + cpos[cur].size(), 1); 
            // 不管怎样，只要有块，总能垒成高度为 1 的塔
            int mx = 1;
            // dp[0 ~ cpos[cur].size()] 中最大的
            int lstod = -1, lstev = -1;
            // 最近的奇数位置和偶数位置，-1 为初始值
            cpos[cur][0] & 1 ? lstod = 0 : lstev = 0;
            // 判断第一个的奇偶性
            for (int i = 1; i < cpos[cur].size(); i++) {
                int lst = cpos[cur][i] & 1 ? lstev : lstod;
                if (lst != -1) 
                    dp[i] = dp[lst] + 1;
                // lst 为第一个奇偶性不同的位置
                mx = max(dp[i], mx);
                cpos[cur][i] & 1 ? lstod = i : lstev = i;
                // 更新最近的奇数位置和偶数位置
            }
            ans[cur] = mx;
        }

        for (int i = 1; i <= n; i++) {
            cout << ans[i] << ' ';
        }
        cout << '\n';
    }
}

C. Qpwoeirut And The City

思路

能发现，不管怎么样，城市中酷的房子最多有 ⌊n−12⌋\lfloor \frac{n - 1}{2} \rfloor 个。

如果是奇数个的话，只有一种排布方法能达到这么多个酷的房子。也就是第一个样例展示的。

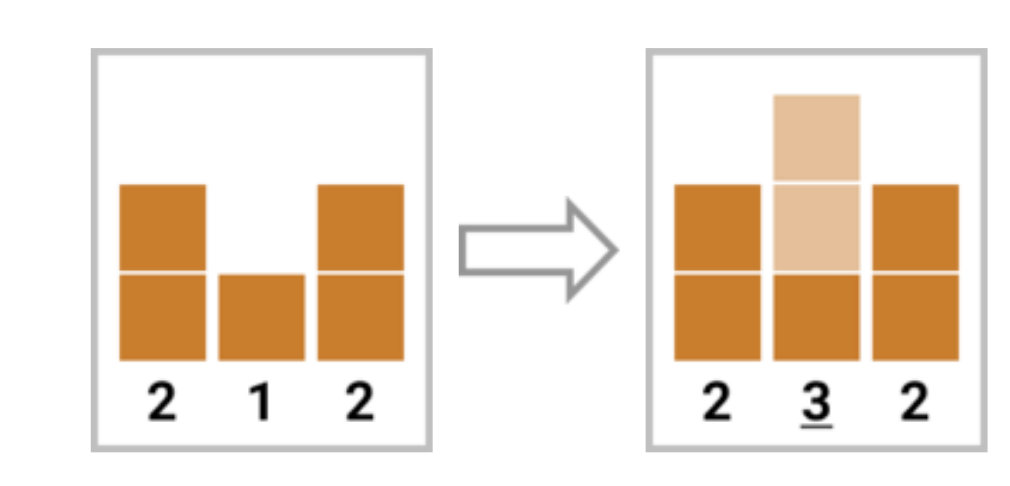
从第二个房子开始，把每个偶数位置的房子都搞成酷的，也就是酷和不酷的房子隔着出现。

计算把一个普通房子变成酷的房子的代价可以用如下方法：

1
2
3
4
5
6
inline ll calc_cost(int i, int* h) {
    if (h[i] <= h[i - 1] || h[i] <= h[i + 1])
        return max(h[i - 1], h[i + 1]) - h[i] + 1;
    else
        return 0;
}

也就是把当前的房子搞的比相邻的最高的房子还要高一格。

但是偶数个房子的情况就比较复杂了。这种情况下 ⌊n−12⌋\lfloor \frac{n - 1}{2} \rfloor 一定等于 n2−1\frac{n}{2} - 1。

那么就会有 n2+1\frac{n}{2} + 1 个不酷的房子，也就一定有两个连在一起出现的不酷的房子，而这两个连续的不酷的房子可以出现在任何位置，我们需要考虑所有的情况。

比如 n=8n = 8 那么有如下几种排布方式。

01010100010100100100101000101010\texttt{010101}\textcolor{red}{\texttt{00}}\\ \texttt{0101}\textcolor{red}{\texttt{00}}\texttt{10}\\ \texttt{01}\textcolor{red}{\texttt{00}}\texttt{1010}\\ \textcolor{red}{\texttt{00}}\texttt{101010}

但是如果从头到尾的把所有情况都计算一遍，时间就不够了。

所以我们可以只计算从一种情况到另一种情况之间代价的变化量。

比如：

01010100↓01010010\texttt{010101}\textcolor{red}{\texttt{00}}\\ \downarrow\\ \texttt{0101}\textcolor{red}{\texttt{00}}\texttt{10}

这个过程中，第六个房子从酷变为不酷，第七个房子从不酷变为酷。

假设我们当前正在把第 ii 个房子从酷变为不酷，第 i+1i + 1 个房子从不酷变为酷。我们只需要调用前面的 calc_cost 减去 ii 的价格再加上 i+1i + 1 的价格就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//author: tzyt
#include <bits/stdc++.h>
using namespace std;
#define ll long long

inline ll calc_cost(int i, int* h) {
    if (h[i] <= h[i - 1] || h[i] <= h[i + 1])
        return max(h[i - 1], h[i + 1]) - h[i] + 1;
    else
        return 0;
}

int main() {
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        int h[n + 1];
        for (int i = 1; i <= n; i++) {
            cin >> h[i];
        }
        ll ans = 0, tmp = 0;
        
        // 奇数情况的解法
        for (int i = 2; i < n; i += 2) {
            ans += calc_cost(i, h);
        }
        if (n & 1) {
            cout << ans << '\n';
            continue;
        }

        tmp = ans;
        for (int i = n - 2; i >= 2; i -= 2) {
            // 枚举连续 0 的位置
            tmp -= calc_cost(i, h);
            tmp += calc_cost(i + 1, h);
            ans = min(ans, tmp);
        }
        cout << ans << '\n';
    }
}

D1. Chopping Carrots (Easy Version)

思路

我们尝试设最小的 ⌊aipi⌋\lfloor \frac{a_i}{p_i} \rfloor 为 mnmn。那么 mn∈[0,a1]mn \in [0, a_1]，因为 pip_i 最小为 11，那 ⌊a11⌋\lfloor \frac{a_1}{1}\rfloor 就是 a1a_1 了。

在这个的基础上，我们再贪心的尝试让每个 ⌊aipi⌋\lfloor \frac{a_i}{p_i} \rfloor 都尽可能的接近 mnmn，这样就可以尽可能的让最大的 ⌊aipi⌋\lfloor \frac{a_i}{p_i} \rfloor 更小。

这样我们就可以算出 pip_i，因为 ⌊aipi⌋≥mn\lfloor \frac{a_i}{p_i} \rfloor \ge mn，所以 pi=⌊aimn⌋p_i = \lfloor \frac{a_i}{mn} \rfloor。当然，pip_i 不能大于 kk，并且如果 mn=0mn = 0，我们就让 pi=kp_i = k。

然后我们去枚举每个可能的 mnmn，并且计算该情况下的最大的 ⌊aipi⌋\lfloor \frac{a_i}{p_i} \rfloor，就能得到答案了。思路好像挺简洁，但是真的挺难想的，

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// author: tzyt
#include <bits/stdc++.h>
using namespace std;
#define IINF 0x3f3f3f3f
int main() {
    int t;
    cin >> t;
    while (t--) {
        int n, k;
        cin >> n >> k;
        int a[n + 1];
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
        }
        int ans = IINF;
        int mxv = 0;
        for (int mnv = 0; mnv <= a[1]; mnv++) {
            // 枚举 mn
            for (int i = 1; i <= n; i++) {
                int p = min(k, (mnv ? (a[i] / mnv) : k));
                // mnv ? (a[i] / mnv) : k 是因为 mnv 为 0 的情况
                mxv = max(mxv, a[i] / p);
            }
            ans = min(ans, mxv - mnv);
        }
        cout << ans << '\n';
    }
}