吐槽一下，官方题解写的挺难看懂的，看了好久还是挺迷糊的（其实也是我太菜了）。搞懂之后感觉这题挺妙的，来写下题解。

思路

我们首先需要有一个观察，就是对于 ss 串，最后一个连续字串不会增加可能的获胜人数。比如 s=0011s = \texttt{0011} 时，后面结尾的 11\texttt{11} 就不会增加可能的获胜人数。

为啥呢，设我们设经过任意次数对战后，玩家可能组合的集合为 tt 那么对于任意的 x∈tx \in t，连续在环境 11 中对战任意次数后，最终的赢家一定是 xx 中温度最高的（因为每个剩下的玩家都会需要连续在环境 11 中对战，唯一能胜出所有对战的玩家一定是最大的）。同理，tt 中的玩家连续在环境 00 中对战任意次数后，最终的赢家一定是 xx 中温度最低的。

例如，s=111s = \texttt{111} 时，最后胜出的一定是 44 号玩家。

这样一来，如果结尾段是 11（00 结尾同理，后面为了方便先用 11 的例子了），我们只需要算出前面的部分最多能构造出多少种最大值（玩家温度）不同的玩家组合，就能知道当前长度的 ss 的答案了。

现在考虑如何构造出最多的最大值不同的玩家组合。如果玩家数量为 nn，那么没有经过任何对战时，最大值就是 nn。想要让最大值不同，只能删除当前的最大值。

特殊情况

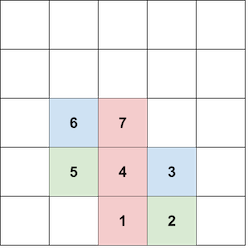
刚刚的描述可能比较抽象，考虑 s=0011s = \texttt{0011} 这个例子就能较好的理解了。

对于第一个 00，除了玩家组合中温度最低的不能删掉（这个不管怎样都能赢），其他的都能删掉（让温度最低的玩家和其他任意玩家对战），共有如下几种情况：

1:123452:123453:123454:123451 : \texttt{1234} \cancel{\texttt{5}} \\ 2 : \texttt{123} \cancel{\texttt{4}} \texttt{5} \\ 3 : \texttt{12} \cancel{\texttt{3}} \texttt{45} \\ 4 : \texttt{1} \cancel{\texttt{2}} \texttt{345} \\

观察发现，只有第一种情况改变了最大值（为啥呢？因为他删掉了最大值）。其他的情况中，必须要连续的删除结尾的一段数字，才能改变最大值。

这时候第二个 00 就起到作用了。对于第二种情况，其可以把 55 删掉，使得玩家组合的最大值变为 33。我们按照这个规律可以进一步推广出这个结论：设结尾段前面连续段的长度为 ll，能产生的最大值不同的玩家组合就为 l+1l + 1，具体来说，可能的最大值范围是 [n−l,n][n - l, n]。（这里 +1+1 是因为可以选择不改变最初的最大值）。

现在为止，我们已经能求出 ss 只有两个连续段时的答案了。即 n−kn - k，其中 k=∣s∣−lk = |s| - l，表示结尾段的长度。

推广

这个时候我们把例子换成 s=1011s = \texttt{1011}，看看例子是否还成立（ss 不止一段）。同样，可以列出第一次对战后的可能玩家组合。因为第一个环境是 11，所以只能删除除了最大值以外的其他玩家：

1:123452:123453:123451:123451 : \texttt{123} \cancel{\texttt{4}} \texttt{5} \\ 2 : \texttt{12} \cancel{\texttt{3}} \texttt{45} \\ 3 : \texttt{1} \cancel{\texttt{2}} \texttt{345} \\ 1 : \cancel{\texttt{1}} \texttt{2345} \\

虽然这些情况中，没有任何一种改变了玩家组合的最大值，但是我们只要在接下来的 00 环境中再对战一次，删除掉 55，就产生了 22 种新的最大值。对于第一种情况，最大值变为了 33，第二种变为了 22。一共也是 n−kn - k 种答案。

那如果段数再多一点呢？比如 s=01011s = \texttt{01011}。这个结论还是成立的。我们可以把 010\texttt{010} 看作一组环境，其中 00 可以删除 [2,n][2, n] 范围内的任何玩家，11 则为 [1,n−1][1, n - 1] 中的任何玩家。把这两种环境组合起来就可以从 [1,n][1, n] 种任意挑选 33 个删除，构造出 44 种不同的最大值（取决于你删除前多少个温度最大的玩家）。

代码和实现

通过前面的例子我们已经分析出了，解决问题只需要知道 ss 的 [1,i][1, i] 子串中，最后一个连续段的长度。不过对于每个 ii 都扫一遍太慢了，需要采用类似动态规划的东西，具体我在代码注释里有解释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){
    int t;
    cin >> t;
    while(t--){
        int n;
        string s;
        cin >> n >> s;
        int cur0len = 0; // 最后一个连续段如果是 0 的话 cur0len 表示其长度，
                         // 如果不是的话 cur0len 就是 0 
        int cur1len = 0; // 和 1 相同
        int curn = 2;    // 最开始是两个玩家
        for (char ch : s){
            int x = ch - '0';
            if (x == 0){
                cur0len++;   // 当前是 0 的话 0 结尾的连续段会比原来更长
                cur1len = 0; // s 的最后一个不是 1 了
            } else {
                cur1len++;
                cur0len = 0;
            }
            cout << curn - (x ? cur1len : cur0len) << " ";
            // 前文中的 n - k
            curn++;
        }
        cout << '\n';
    }
}